控制系统的结构图如图5-29所示。其开环传递函数为

图5-29 控制系统结构图
![]()
因此,开环频率特性为
![]()
由于线性定常系统分子多项式与分母多项式均为常系数,可以将开环频率特性G0(jω)的分子多项式与分母多项式作因式分解如下式

式(5-70)包括比例因子、一阶因子和二阶共轭复数因子,都是基本环节,所以G0(jω)的一般表达式可以写为基本因子的乘积,即
![]()
采用模、角表达式可表示为
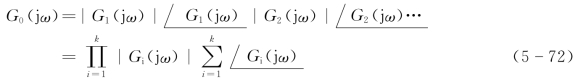
开环对数幅频特性为

开环对数相频特性为

式(5-73)和式(5-74)说明了L0(ω)和φ0(ω)分别都是各典型环节的叠加。
通过以上的分析,可以采用下述两种方法中的任意一种方法,来绘制控制系统的开环对数频率特性,也就是波德图。但使用更多的还是后一种方法。
1.典型环节叠加作图
分别作出各基本环节的Li(ω),在图上叠加得到L0(ω),以及分别作出各基本环节的φi(ω),在图上叠加得到φ0(ω)。
【例5-3】 已知单位负反馈控制系统如图5-30所示,其开环传递函数为

图5-30 控制系统结构图
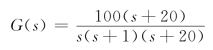
试绘制开环系统波德图。
解:按照基本环节写出系统的开环频率特性为

各基本环节为
1)G1(jω)=10L1(ω)=20lg10=20dB
φ1(ω)=0°
两条特性曲线均为水平线,幅频特性的高度为20dB。
2)G2(jω)=1+j0.5ωL2(ω)=![]()
φ2(ω)=arctan0.5ω
一阶微分环节,转折频率为![]() ,转折斜率为+20dB/dec。
,转折斜率为+20dB/dec。
3)G3(jω)=![]() L3(ω)=-20lgω
L3(ω)=-20lgω
φ3(ω)=-90°
积分环节,等斜率斜线,斜率为-20dB/dec。
4)G4(jω)=![]() L4(ω)=
L4(ω)=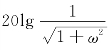
φ4(ω)=-arctanω
一阶惯性环节,转折频率为ω=1,转折斜率为-20dB/dec。
5)G5(jω)=
φ5(ω)=-arctan0.05ω
一阶惯性环节,转折频率为![]() ,转折斜率为-20dB/dec。
,转折斜率为-20dB/dec。
各基本环节的对数幅频特性如图5-31所示。在图上作叠加合成,即可得到
L(ω)=L1(ω)+L2(ω)+L3(ω)+L4(ω)+L5(ω)(https://www.xing528.com)
如图5-31所示。

图5-31 对数幅频特性
同理,作出各基本环节的对数相频特性如图所示,经叠加合成,可以得到
φ(ω)=φ1(ω)+φ2(ω)+φ3(ω)+φ4(ω)+φ5(ω)
如图5-32所示。

图5-32 对数相频特性
2.转折渐进作图
转折渐进作图主要是依照转折渐进法作出L0(ω),而开环对数相频特性φ0(ω)仍然要依照方法(1)叠加作图。但是从后面的分析可以看到,在许多情况下,可以省略φ0(ω)的作图。这样,转折渐进作图就又快又方便了。
具体作图步骤可归纳如下:
(1)将开环传递函数写成尾一型标准形式。
(2)根据比例环节,求出20lgK0。
(3)过ω=1,L(ω)=20lgK0,即(1,20lgK0)作一条斜率为-20υdB/dec的斜线(υ是积分环节的个数)。
(4)计算各典型环节的转折频率![]() ,并按ωi 由小到大的顺序,依次改变各对应频段的斜率,并依次叠加,即得出最后的对数幅频特性。
,并按ωi 由小到大的顺序,依次改变各对应频段的斜率,并依次叠加,即得出最后的对数幅频特性。
(5)作各环节对数相频特性,并依次叠加得到最后的对数相频特性。
【例5-4】 单位负反馈系统开环传递函数如下,绘制系统对数幅频特性曲线的渐近线。
![]()
解:1)把开环传递函数化为尾一型标准形式

2)20lgK0=20lg7.5=17.5(dB)。
3)过(1,17.5)作斜率为-20dB/dec的斜线。
4)求各转折频率(见表5-2)。
表5-2

5)依次作图如图5-33所示。

图5-33 例5-4 系统的对数幅频特性曲线
【例5-5】 已知单位负反馈系统的开环传递函数为
![]()
作对数开环频率特性。
解:1)首先,把开环传递函数化为尾一型标准形式,其次,求20lgK0=20lg1.58=3.97。
2)过(1,3.97)作斜率为-20υdB/dec=-20dB/dec的斜线。
3)求各转折频率并作表(见表5-3)。
表5-3

4)依次作图如图5-34所示。
另外,由于二阶振荡因子的阻尼比为ζ=0.2,所以,在谐振频率![]() 1.918 处,谐振峰值为
1.918 处,谐振峰值为

对数峰值为
20l g2.55=8.13(dB)
在图上作谐振峰值修正曲线如图5-34所示。

图5-34 例5-5 系统的波德图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




