典型环节频率特性优化

由于对数频率特性是频率法分析的主要工具，且根据作图特点，很容易掌握草图的徒手绘制方法。因此，本节叙述各典型环节的绘图要点及绘图方法。

设线性定常系统结构如图5-6所示，其开环传递函数为G（s）H（s），为了绘制系统开环频率特性曲线，本节先研究开环系统的典型环节及相应的频率特性。

图5-6　典型系统结构图

1.典型环节

由于开环传递函数的分子和分母多项式的系数皆为实数，因此系统开环零极点或为实数或为共轭复数。根据开环零极点可将分子和分母多项式分解成因式，再将因式分类，即得典型环节。典型环节可分为两大类。一类为最小相位环节；另一类为非最小相位环节。最小相位环节有下列七种：

（1）比例环节K（K＞0）。

（2）惯性环节1/（Ts＋1）（T＞0）。

（3）一阶微分环节Ts＋1（T＞0）。

（4）振荡环节1/（s2/ω2n＋2ζs/ωn＋1）（ωn＞0，0≤ζ＜1）。

（5）二阶微分环节s2/ω2n＋2ζs/ωn＋1（ωn＞0，0≤ζ＜1）。

（6）积分环节1/s。

（7）微分环节s。

非最小相位环节共有五种：

（1）比例环节K（K＜0）。

（2）惯性环节1/（－Ts＋1）（T＞0）。

（3）一阶微分环节－Ts＋1（T＞0）。

（4）振荡环节1/（s2/ω2n－2ζs/ωn＋1）（ωn＞0，0＜ζ＜1）。

（5）二阶微分环节s2/ω2n－2ζs/ωn＋1（ωn＞0，0＜ζ＜1）。

除了比例环节外，非最小相位环节和与之对应的最小相位环节的区别在于开环零极点的位置。非最小相位（2）～（5）环节对应于s 右半平面的开环零点或极点，而最小相位（2）～（5）环节对应于s 左半面的开环零点或极点。

2.典型环节的频率特性

（1）比例环节。频率特性为

1）极坐标图。幅值为

相角为

其极坐标图如图5-7所示。

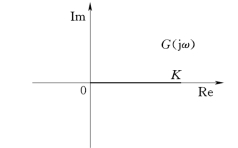
图5-7　比例环节的极坐标图

2）波德图。由于

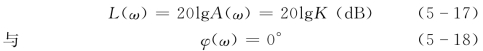
在波德图上的两条曲线分别为水平线，如图5-8所示。

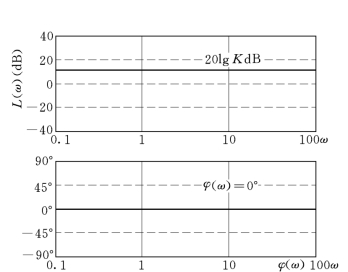
图5-8　比例环节的波德图

（2）积分环节。频率特性为

1）极坐标图。幅频特性为

相频特性为

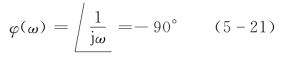
当ω由0＋→∞时，其相角恒为－90°，幅值的大小与ω成反比。因此，曲线在负虚轴上。积分环节的极坐标图如图5-9所示。

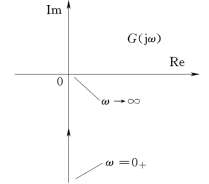
图5-9　积分环节的极坐标图

2）波德图。对数幅频特性L（ω）表达式为

因此曲线为每十倍频衰减20dB的一条斜线，是等斜率变化的。

对数相频特性φ（ω）表达式为

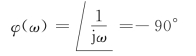
因此，在图上是相角为－90°的一条直线。积分环节的对数频率特性如图5-10所示。

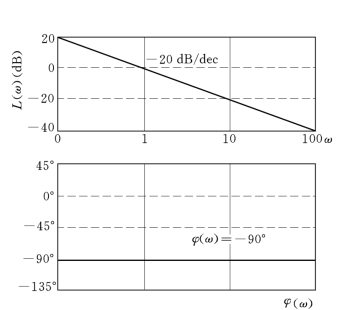
图5-10　积分环节的波德图

（3）微分环节。微分环节的频率特性为

1）极坐标图。幅值为

相角为

微分环节的极坐标图如图5-11所示。当ω由0＋→∞时，其相角恒为＋90°，幅值的大小与ω成正比。因此，曲线在正虚轴上，与积分环节的极坐标图对称。

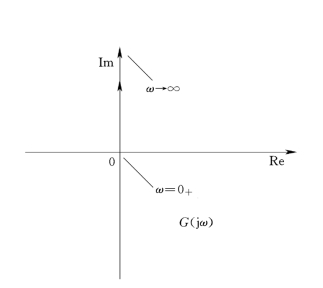
图5-11　微分环节的极坐标图

2）波德图。对数幅频特性L（ω）表达式为

可见，与积分环节相反，等斜率值为每十倍频增加20dB。

对数相频特性为

因此，在图上是相角为＋90°的一条直线。微分环节的对数幅频特性与对数相频特性如图5-12所示。

图5-12　微分环节的波德图

（4）惯性环节。惯性环节的频率特性为

1）极坐标图。实部与虚部表达式为

其模角表达式为

幅值为

极限值为

相角为

极限值为

依照上述趋势分析可以作出惯性环节的极坐标图如图5-13所示。

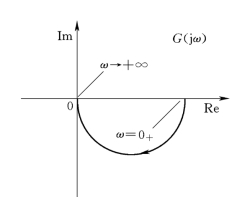
图5-13　惯性环节极坐标图

2）波德图。对数幅频特性为

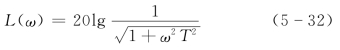
幅频特性曲线如图5-14所示。如果徒手近似作图，可以采用渐近线作图。首先确定它的两条渐近线。由于

当频率趋于零时，是一条水平渐近线。由于

当频率趋于无穷大时，是一条等斜率渐近线，斜率为每十倍频衰减20dB。

两条渐近线的交点处的频率称为转折频率，其坐标为

3）对数相频特性。惯性环节的相频特性表达式为

它有三个特征角如下：

当频率ω→0 时，有φ（ω）→0°。

当频率时，有φ（ω）→－45°。

当频率ω→∞时，有φ（ω）→－90°。

由于对于所有的频率有

相频特性φ（ω）是单调减的，而且以转折频率为中心，两边的角度是反对称的。依照上述分析作出惯性环节的相频特性曲线如图5-14所示。

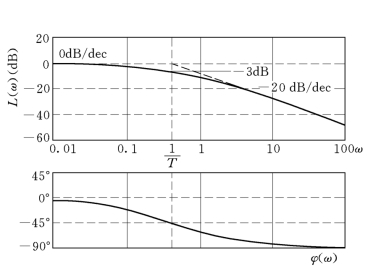(www.xing528.com)

图5-14　惯性环节波德图

从对数幅频特性L（ω）上可以看出，用渐近线作图是有近似误差的，最大误差发生在转折频率处。将其坐标代入表达式L（ω），可以算出最大误差为

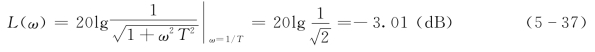
因最大误差两端的误差值是对称的，故可以作出误差修正曲线如图5-15所示，来对渐近线作图所产生的误差进行修正。

图5-15　惯性环节折线误差曲线

从误差曲线可以看到。在转折频率处，最大误差为－3.01dB，两端十倍频程处的误差降到－0.04dB。所以两端十倍频程之外的误差可以忽略不计。

（5）一阶微分环节。一阶微分环节的频率特性为

1）极坐标图。幅频特性为

相频特性为

当频率ω由0 变到∞时，实部始终为单位1，虚部则随着ω线性增长。所以，它的极坐标图比较特殊如图5-16所示。

图5-16　一阶微分环节的极坐标图

2）波德图。对数幅频特性为

对数相频特性为

从上面的表达式可以看出，由于一阶微分环节与一阶惯性环节的对数频率特性是上下对称的，可以利用一阶惯性环节的对数频率特性作上下翻转画出。其对数频率特性曲线如图5-17所示。

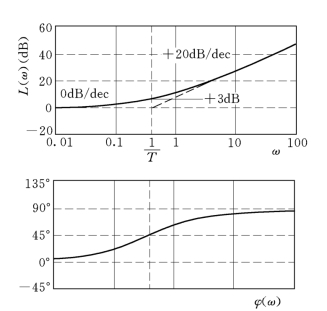
图5-17　一阶微分环节的波德图

（6）二阶振荡环节。二阶振荡环节的传递函数为

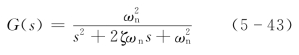
令为二阶系统的时间常数，代入式（5-43）有

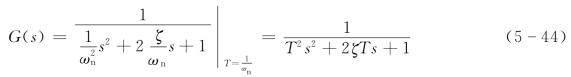
所以，二阶振荡环节的频率特性为

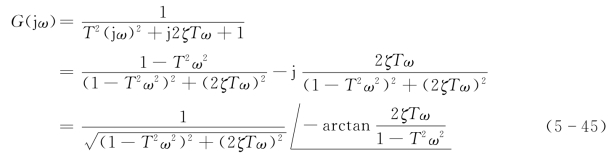
幅频特性为

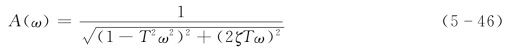
相频特性为

其极坐标图如图5-18所示。

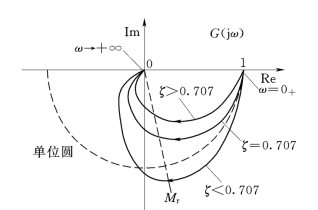
图5-18　二阶振荡环节的极坐标图

从图中可以看到，当ω→0＋时

A（0）＝1，φ（ω）＝0°

由于频率增加时，相角是单调减的，所以曲线从实轴上出发，射向第四象限。

当ω＝＋∞时

A（＋∞）＝0，φ（＋∞）＝－180°

所以曲线的模拟相角－180°趋于零。

另外，从图上可以看到，有的曲线的模超出了单位圆。可以求得在系统参数所对应的条件下，在某一振荡频率ω＝ωr 处，二阶振荡环节会产生谐振峰值Mr。

在产生谐振峰值处，必有

因此，可以解出谐振频率为

将其代入幅值表达式，求得谐振峰值为

及无峰值时的系统参数临界值为

ωr＝0，ζ＝0.707

ζ＞0.707，ζ＝0.707和ζ＜0.707的无谐振峰值、临界谐振峰值和有谐振峰值的三条极坐标图的曲线如图5-18中所示。

对数幅频特性表达式为

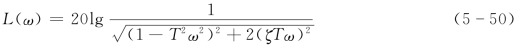
根据式（5-50）可以作出两条渐近线。

这是一条水平渐近线，又，频率趋于无穷大时有

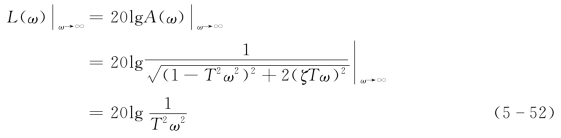
显然，上式为两个积分环节的叠加。

所以第二条渐近线为等斜率的斜线，其斜率为两个积分环节的斜率叠加，即斜率为－40dB/dec。

在图上作出两条渐近线，得到它们的交点坐标为

两条渐近线的折线近似如图5-19虚线所示。

由于阻尼比ζ不同时，幅频特性L（ω）为无谐振峰值、临界谐振峰值和有谐振峰值三种情况，阻尼比分别为

ζ＞0.707

ζ＝0.707

ζ＜0.707

时，幅频特性L（ω）的准确曲线如图5-19所示。

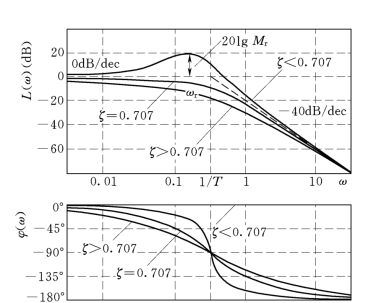
图5-19　二阶振荡环节的波德图

对数相频特性表达式为

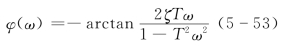
二阶振荡环节的对数相频特性也有三个特征角度。

当ω→0 时，有φ（0）＝0°

当时，有

当ω→∞时，有＝－180°

并且由于系统阻尼比ζ取值不同，φ（ω）在邻域的角度变化率也不同，阻尼比越小，变化率就越大。阻尼比分别为ζ＞0.707，ζ＝0.707 和ζ＜0.707 时三条相频特性如图5-19所示。

（7）二阶微分环节。二阶微分环节的频率特性为

它的极坐标图如图5-20所示。

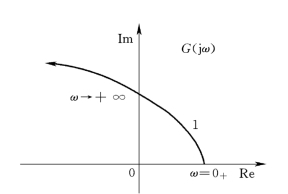
图5-20　二阶微分环节的极坐标图

由于二阶微分环节与二阶振荡环节互为倒数，因此，其波德图可以参照二阶振荡环节的波德图翻转画出如图5-21所示。

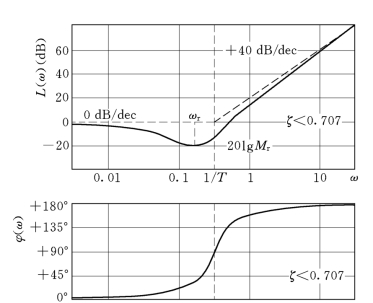
图5-21　二阶微分环节的波德图

说明：

（1）非最小相位环节和对应的最小相位环节。对于每一种非最小相位的典型环节都有一种最小相位环节与之对应，其特点是典型环节中的某个参数的符号相反。

最小相位的比例环节G（s）＝K（K＞0），简称为比例环节，其幅频和相频特性为

非最小相位的比例环节G（s）＝－K（K＞0），其幅频和相频特性为

最小相位的惯性环节，其幅频和相频特性为

非最小相位的惯性环节，又称为不稳定惯性环节，，其幅频和相频特性为

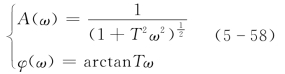
由式（5-57）和式（5-58）可知，最小相位惯性环节和非最小相位的惯性环节，其幅频特性相同，相频特性符号相反，极坐标图关于实轴对称；对数幅频曲线相同，对数相频曲线关于0°线对称。上述特点对于振荡环节和非最小相位（或不稳定）振荡环节、一阶微分环节和非最小相位一阶微分环节、二阶微分环节和非最小相位二阶微分环节均适用。

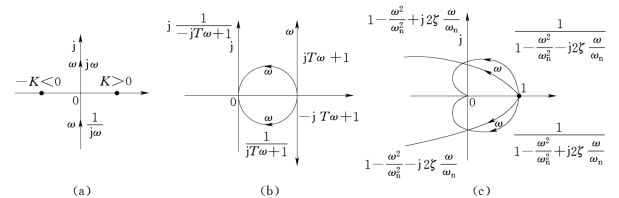
图5-22　典型环节极坐标图

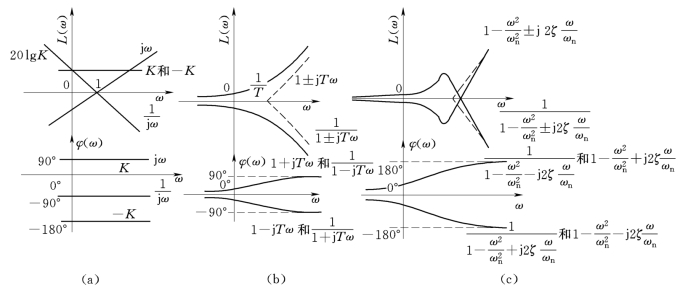
图5-23　典型环节的波德图

（2）传递函数互为倒数的典型环节。最小相位典型环节中，积分环节和微分环节、惯性环节和一阶微分环节、振荡环节和二阶微分环节的传递函数互为倒数，即有下述关系成立

设G1（jω）＝A1（ω）ejφ1（ω），则

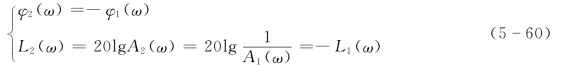
由此可知，传递函数互为倒数的典型环节，对数幅频曲线关于0dB 线对称，对数相频曲线关于0°线对称。在非最小相位环节中，同样存在传递函数互为倒数的典型环节，其对数频率特性曲线的对称性亦成立。