频率特性的数学表示和作图方法

在工程分析和设计中，通常把频率特性画成一些曲线，通过这些曲线对系统进行研究，常用的一些曲线有：幅频特性曲线、相频特性曲线、极坐标图、对数频率特性坐标图。下面以RC 网络为例来画这组曲线。

1.幅频特性、相频特性曲线

由式（5-11）可知RC 网络的频率特性

RC 网络的幅频、相频随输入正弦频率ω变化的数据见表5-1。表5-1幅频特性和相频特性数据。

表5-1　幅频特性和相频特性数据

（1）幅频特性。以频率ω为横坐标，以幅频A（ω）为纵坐标，画出A（ω）随频率ω变化的曲线，称为幅频特性曲线。按表5-1的数据画出RC 网络的幅频特性曲线如图5-2所示。

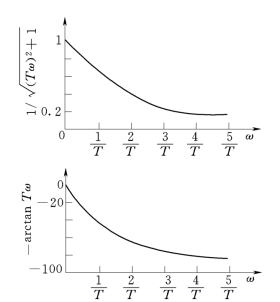
图5-2　RC 网络的幅频特性与相频特性

（2）相频特性。以频率ω为横坐标，以相频φ（ω）为纵坐标，画出φ（ω）随频率ω变化的曲线，称相频特性曲线。按表5l 的数据，画出RC 网络的相频特性曲线如图5-2所示。

2.极坐标图

极坐标图又称幅相图、幅相曲线、奈奎斯特（NyquiSt）图，简称奈氏图。是指当频率从－∞到＋∞区间变化时，复数的向量终端轨迹。

极坐标曲线是将频率ω作为参变量，将幅频与相频特性同时表示在复数平面上。图上实轴正方向为相角的零度线，逆时针方向转过的角度为正角度，顺时针方向转过的角度为负角度。对于一个确定的频率，必有一个幅频的幅值和一个相频的相角与之对应，例如，表5-1中在时，A（ω）＝0.707、φ（ω）＝－45°。根据A（ω）与φ（ω）的值，在复数平面上画出一个向量。当频率ω由零变到无穷大时，可在复数平面上画出一组向量，将这一组向量的终端连成一条曲线，即为极坐标图。RC 网络的极坐标图如图5-3所示。

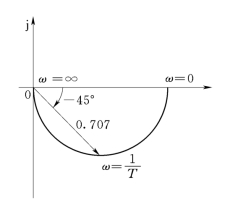
图5-3　RC 网络的极坐标图

3.对数频率特性曲线

为了较方便的绘制频率特性曲线，常将幅频与相频特性画在对数坐标上，这种几何表示方法应用十分广泛。(www.xing528.com)

对数频率特性曲线又称波德（Bode）图，它包括对数幅频特性与对数相频特性两条曲线。

（1）对数幅频特性。对数幅频特性的纵坐标是以幅频A（ω）取对数（以10 为底）后再乘以20，即20lgA（ω），用L（ω）表示，单位为分贝（用 dB）表示。即 L（ω）＝20lgA（ω）dB，横坐标按lgω刻度，但标注的数字是真数ω，由于是按以10 为底的对数刻度，因此，频率每变化十倍，横坐标轴上就变化一个单位长度，称为“十倍频程”，用dec表示。对数刻度是不均匀的刻度。

（2）对数相频特性。对数相频特性的纵坐标表示相频特性φ（ω）值，是线性刻度，单位是“度”。横坐标是以lgω刻度，标注的仍然是真数ω，与对数幅频特性的横坐标相同。图5-4为对数坐标刻度图。

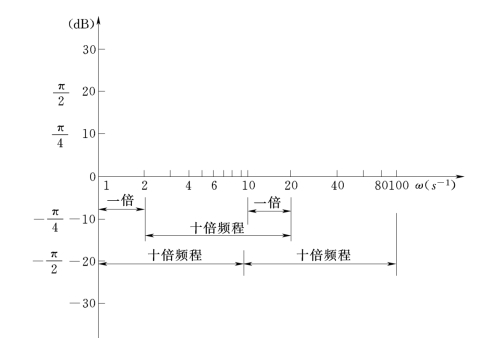
图5-4　对数坐标刻度图

对数频率特性有许多优点，因此在波德图上来展示控制系统的各种性能是非常方便的。其优点如下所述。

（1）波德图可以双重展宽频带。由于横坐标ω轴作了对数变换，其效果是：将高频频段各十倍频程拉近，展宽了可视频带宽度。另一方面，又将低频频段的各十倍频程分得很细，展宽了表示频带宽度，便于细致观察幅值、相角随频率变化的程度与变化的趋势。

（2）基本环节都可以由渐近线画出。如图5-5所示，RC 网络构成的惯性环节，其L（ω）曲线就是由两条渐近线构成的，且仅在两条渐近线的交点处产生较小误差，因此作出的曲线比较准确。

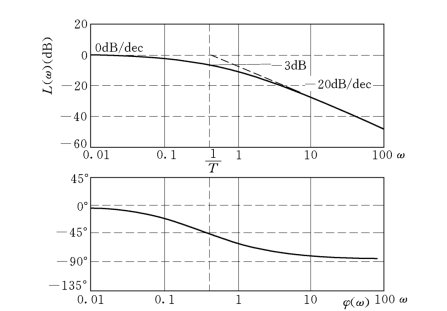
图5-5　RC 网络的对数幅频特性和相频特性曲线

（3）叠加作图。控制系统的频率特性一般为因子相乘，如

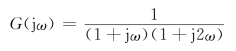
其对数幅频特性为

其对数相频特性为

由于L（ω），φ（ω）都是各因子特性的叠加，因此作图方便。