频率特性定义及其在线性定常系统中的应用

线性定常系统，在正弦信号作用下，稳态输出的振幅与输入振幅之比，仅与频率ω有关，称为幅频特性，用A（ω）表示。稳态输出的相位与输入相位之差，仅与频率ω有关，称相频特性，用φ（ω）表示，即

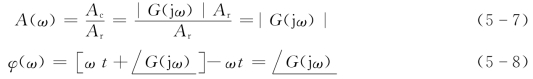
幅频A（ω）与相频φ（ω）统称频率特性，即

如果将输入、输出的正弦函数用电路理论中的符号法表示，即输入为Arej0，输出为Acejφ，则输出与输入的复数之比为

所以，频率特性可定义为：线性定常系统，在正弦信号作用下，输出的稳态分量与输入的复数比，称为系统的频率特性（即为幅相频率特性，简称极坐标）。

不难证明，频率特性与传递函数之间有着确切的简单关系，即

将传递函数中的复变量s 用jω代换后，即可得到频率特性表达式。

下面以RC 网络为例求频率特性，RC 网络如图5-1所示。其传递函数为

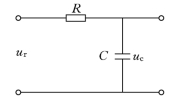
图5-1　RC 网络图

(www.xing528.com)

其中T＝RC

将式（5-10）中的s 用jω代换，得频率特性

幅频特性为

相频特性为

从式（5-13）看出，幅频与相频特性都是输入正弦频率ω的函数。

关于频率特性的几点说明：

（1）频率特性不只是对系统而言，其概念对控制元件、部件、控制装置均适用。

（2）频率特性只适用于线性定常系统，否则不能用拉氏变换求解，也不存在这种稳态对应关系。

（3）前面在推导频率特性时，是在假定线性微分方程稳定的条件下导出的。如果不稳定，则动态过程c（t）最终不可能趋于稳态振荡cS（t），当然也就无法由实际系统直接观察到这种稳态响应。但从理论上推导动态过程时它的稳态分量总是可以分离出来的，而且其规律性并不依赖于系统的稳定性。因此可以扩展频率特性的概念，将频率特性定义为：在正弦输入下，线性定常系统输出的稳态分量与输入的复数比，以G（jω）或Φ（jω）表示。

（4）由频率特性的表达式G（jω）可知，其包含了系统或元部件的全部结构和参数。故尽管频率特性是一种稳态响应，而动态过程的规律性必将寓于其中。所以频率法就是运用稳态的频率特性间接研究系统的动态响应，从而避免了直接求解高阶微分方程的困难。

频率特性与微分方程和传递函数一样，也是系统或元件的动态数学模型。