开环极点变化引起的根轨迹变化

设单位负反馈系统的开环传递函数为

式中，K*为开环根轨迹增益，而P1 是系统的开环极点。现在研究P1＝0→∞变化的根轨迹，显然这也是广义根轨迹，它的等效开环传递函数为

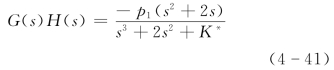
根据等效开环传递函数式（4-41）可以画出开环极点P1 变化时的广义根轨迹。

【例4-9】 已知系统的开环传递函数为

试绘制当开环增益K 为，1，2 时，时间常数Ta＝0→∞变化时的根轨迹。

解：求Ta 从零到无穷变化时的闭环根轨迹，显然是求广义根轨迹，而且K 为不同值，则将是一簇广义根轨迹。系统特征方程为

D（s）＝s（s＋1）（Tas＋1）＋K＝0

等效开环传递函数为

等效开环传递函数有3 个零点，即z1＝0，z2＝0，z3＝－1，有2 个极点，根据不同的K值可计算出极点为：

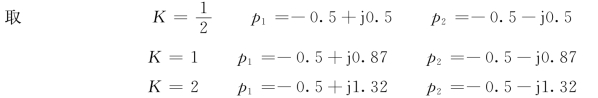
然后根据常规根轨迹的绘制法则可绘制出广义根轨迹。

（1）n＝2，m＝3，则有3 条根轨迹。

（2）起于开环有限极点P1，P2，和无限远极点，终于开环零点z1，z2，z3。(https://www.xing528.com)

（3）实轴上根轨迹在（－1，－∞）区间。

（4）求出射角与入射角。当K 为不同值时，可分别计算出出射角与入射角：

出射角：

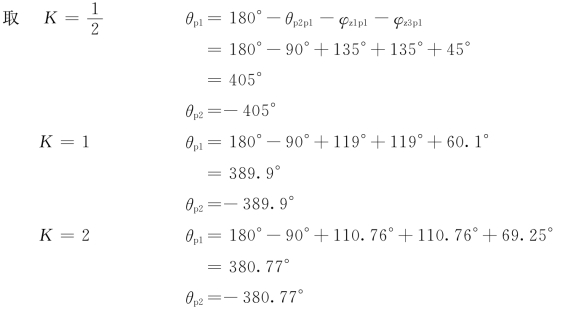
入射角：没有复数零点，可不求入射角。

（5）与虚轴的交点，当取不同K 值时利用s＝jω，求解特征方程方法，可求出与虚轴相交时的Ta 值和ω值。系统闭环特征方程为

D（s）＝Tas2（s＋1）＋s2＋s＋K＝0

令s＝jω，代入上式，可得方程组

－Taω3＋ω＝0

－Taω2－ω2＋K＝0

求解方程组，可得：

取K＝时，Ta 和ω无解，则无交点。

K＝1 时，Ta 和ω无解，则无交点。

K＝2 时，Ta＝1，ω＝±1。

根轨迹如图4-17所示。

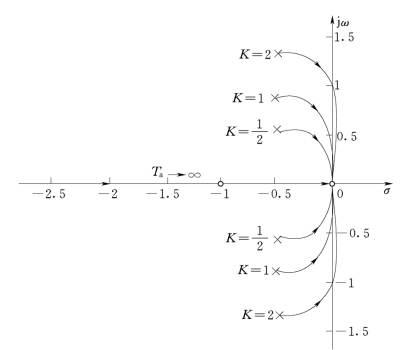
图4-17　例4-9 题根轨迹图