根轨迹中根的和与积的关系

如果系统的特征方程写成如下形式：

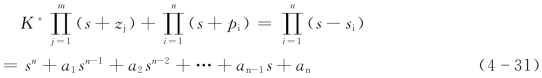
式中－zj、－Pi——开环零、极点；

si——闭环极点。

结论如下：

（1）闭环特征根的负值之和，等于闭环特征方程式的第二项系数a1。若（n－m）≥2，根之和与开环根轨迹增益K*无关。

（2）闭环特征根之积乘以（－1）n，等于闭环特征方程的常数项。上述的结论写成表达式，即

这是显然的，不需证明。这里只是告诉读者当（n－m）≥2 时，根之和与K*无关，是个常数，这样，当K*增加时，闭环的根如果有一部分向左移动，就一定相应的有一部分向右移动，使其根之和保持不变。另外也可以根据根之和和根之积的关系确定出闭环极点。

法则8 若系统的特征方程可写为：D（s）＋KgN（s）＝sn＋A1sn－1＋A2sn－2＋…＋An＝0，则对于Kg 的每一个确定值，根轨迹上的各对应点之和为s1＋s2＋…＋sn＝－A1，各对应点之积为s1s2…sn＝（－1）nAn。

图4-14画出了常见闭环系统的根轨迹图。

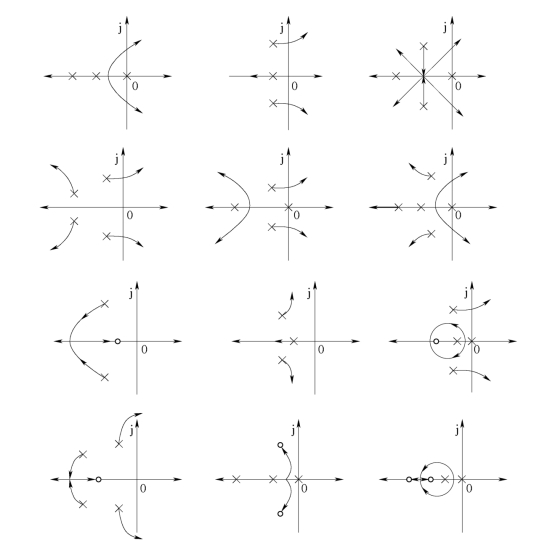
图4-14　常见闭环系统的根轨迹图

【例4-7】 已知单位负反馈系统开环传递函数为

试画出K＝0→∞时的闭环系统的概略根轨迹，并求出K＝K临时的闭环传递函数及闭环极点。

解：首先把尾一型传递函数化成首一型为

根据根轨迹绘制的基本法则，按步计算出各个有关参数，然后绘制根轨迹。

（1）n＝4，有四条根轨迹。

（2）起始于开环极点0，－20，－2－j4，－2＋j4，终于无穷远处。

（3）实轴上的根轨迹在（0，－20）区间。

（4）n＝4，m＝0，则有四条根轨迹趋于无穷远，它们的渐近线与实轴的交点和夹角为

（5）根轨迹的出射角。由于开环传递函数没有零点，则只需计算出射角，设两个复极点为－P3，－P4，相应的出射角为

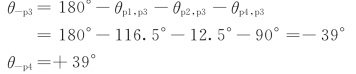
（6）分离点坐标d。根据分离点的性质，在区间（0，－20）之间必有分离点，则用试探法有(www.xing528.com)

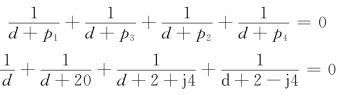
解上述方程，得到

d1＝－15.1，d2＝－1.45＋j2.07，d3＝－1.45－j2.07

舍去d2，d3，所以，d1＝－15.1。

（7）根轨迹与虚轴交点。根据渐近线与实轴的夹角可知，一定有两条根轨迹通过虚轴。根据特征方程，用劳斯判据或令s＝jω的方法，可以求出与虚轴相交处的Kg 与ω值。根轨迹通过虚轴时的开环增益K 称为K临。

系统特征方程为

D（s）＝s（s＋20）（s2＋4s＋20）＋Kg＝s（s＋20）（s2＋4s＋20）＋400K＝0

令s＝jω，代入上式，将虚部和实部分别写成方程式如下

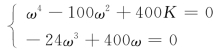
解上面方程组，得

ω1＝0，ω2＝4.1，ω3＝－4.1，K临＝3.47

根轨迹如图4-15所示。

图4-15　例4-7 题根轨迹图

当K＝K临＝3.47 时，此时两个闭环极点s1＝j4.1，s2＝－j4.1，而另外两个闭环极点可由特征方程求出。此时特征方程为

D（s）＝s（s＋20）（s2＋4s＋20）＋400K临＝0

D（s）＝s4＋24s3＋100s2＋400s＋1388.9＝0

利用综合除法，可求出其他两个闭环极点，因为

D（s）＝（s－s1）（s－s2）（s－s3）（s－s4）＝0

式中s1，s2，s3，s4 为闭环极点，而s1，s2 已知，则

所以

s3＝－4.2，s4＝－19.8

闭环系统传递函数为

本题也可以利用幅值条件方程，用试探法求出其他两个闭环极点。