当系统的开环极点和零点位于复平面上时,根轨迹离开共轭复数极点的出发角称为根轨迹的出射角,根轨迹趋于共轭复数零点的角称为根轨迹的入射角。根据根轨迹的相角条件,可求得根轨迹的出射角和入射角。
设系统的开环极点和零点如图4-11所示。其中-P1,-P2 为共轭复数极点,两支根轨迹以θ1c 和θ2c 的出射角离开-P1 和-P2。
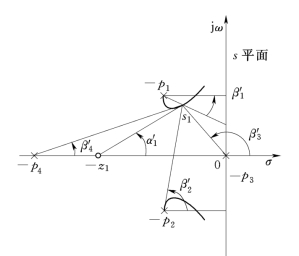
图4-11 出射角和入射角
在离开-P1 的根轨迹上取一点s1,s1 应满足如下相角条件,即
α′1-(β′1+β′2+β′3+β′4)=±180°(2k+1)
则
β′1=∓180°(2k+1)+α′1-(β′2+β′3+β′4)
当s1 点趋于-P1 时,β′1 即为根轨迹离开-P1 点的出射角,β′1 趋于θ1c,而α′1、β′2、β′3 和β′4 也分别趋于各开环零点和极点相对于-P1 点的向量的相角α1、β2、β3 和β4。这时
θ1c=∓180°(2k+1)+α1-(β2+β3+β4)
一般情况下,根据根轨迹方程的相角条件可求得根轨迹离开复数极点-Px 的出射角θxc为

同理,进入复数零点-zy 的根轨迹的入射角θyr为

法则6 根轨迹的出射角和入射角可用如下公式确定:

式中 θxc——根轨迹离开复数极点-Px的出射角;
θyr——根轨迹趋于复数零点-zy的入射角;
αj——-Px(-zy)与各零点的夹角;(https://www.xing528.com)
βi——-Px(-zy)与各极点的夹角。
αj,βi 是由各零极点指向-Px(-zy)的有向线段与实轴正向的夹角。
【例4-5】 设系统开环传递函数为
![]()
试绘制该系统概略根轨迹。
解:将开环零、极点画在图4-12中。按如下步骤绘制根轨迹:
(1)定实轴上的根轨迹。本例实轴上区域[0,-1.5]和[-2.5,-∞]为根轨迹。
(2)确定根轨迹的渐近线。本例n=4,m=3,故只有一条趋于180°的渐近线,它正好与实轴上的根轨迹区域[-2.5,-∞]重合,所以在n-m=1 的情况下,不必再去确定根轨迹的渐近线。
(3)确定分离点。一般说来,如果根轨迹位于实轴上一个开环极点和一个开环零点(有限零点或无限零点)之间,则在这两个相邻的零、极点之间,或者不存在任何分离点,或者同时存在离开实轴和进入实轴的两个分离点。本例无分离点。
(4)确定出射角与入射角。本例概略根轨迹如图4-12所示,为了比较准确地画出这一根轨迹图,应当确定根轨迹的出射角和入射角的数值。先求出射角。作各开环零、极点对(-0.5+j1.5)的向量,并测出相应角度,如图4-13(a)所示。按式(4-29)算出根轨迹在极点(-0.5+j1.5)处的出射角为

图4-12 例4-5 系统的概略根轨迹图
θp1=180°+(φ1+φ2+φ3)-(θ1+θ2+θ3)=79°
根据对称性,根轨迹在极点(-0.5-j1.5)处的出射角为-79°。
用类似方法可算出根轨迹在复数零点(-2+j)处的入射角为149.5°。各开环零、极点到(-2+j)的向量相角如图4-13(b)所示。

图4-13 例4-5 根轨迹的出射角和入射角
(a)出射角;(b)入射角
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




