根轨迹的会合与分离点

若干条根轨迹在复平面上的某一点相遇后又分开，称该点为分离点或会合点。如图4-7所示某系统的根轨迹图，由开环极点－P1 和－P2 出发的两支根轨迹，随Kg 的增大在实轴上A点相遇后即分离进入复平面。随着Kg 的继续增大，又在实轴上的B点相遇并分别沿实轴的左右两方向运动。当Kg趋于无穷大时，一支根轨迹终止于开环零点－z，另一支根轨迹趋于实轴的负无穷远处。实轴上有两个交点A 和B，分别称为根轨迹在实轴上的分离点和会合点。

图4-7　分离点与会合点

1.实轴分离点和会合点的判别

如果实轴上两个相邻开环极点之间是根轨迹（由实轴根轨迹的判别得到），则它们之间必有分离点；如果实轴上两个相邻开环零点（其中一个可为无穷远零点）之间是根轨迹，则这两相邻零点之间必有会合点。如果实轴上根轨迹在开环零点与极点之间，则它们中间可能既无分离点也无会合点，也可能既有分离点也有会合点。

在分离点或会合点上，根轨迹的切线和实轴的夹角称为分离角。分离角θd 与相分离的根轨迹的分支数K 有关，即

例如，实轴上两支根轨迹的分离角为±90°。三支根轨迹的分离角为0°、±60°、±180°。式（4-18）的分离角公式可以由相角条件公式证得。

2.分离点或会合点位置的计算

分离点或会合点位置的计算可用重根法、极值法或其他方法来求取。

（1）重根法。

几条根轨迹在复平面上某点相遇又分开，该点必为特征方程的重根点。如两条根轨迹相遇又分开，该点为二重根。三条根轨迹相遇又分开，该点为三重根等。重根的确定可以借助于代数重根法则：

已知n 次代数方程为

方程（4-19）有n 个根。若n 个根全部是单根，则满足其导数方程ƒ′（x）＝0 的根不是原方程ƒ（x）＝0 的根。

如果方程（4-19）有二重根，则满足其一阶导数方程ƒ′（x）＝0 的根含有原方程ƒ（x）＝0的根。

如果方程（4-19）有三重根，则满足其一阶导数方程ƒ′（x）＝0 的根含有原方程ƒ（x）＝0的根，且满足其二阶导数方程ƒ〞（x）＝0 的根也含有原方程ƒ（x）＝0 的根。

如果方程（4-19）有m 重根，则满足其一阶导数方程ƒ′（x）＝0 的根，二阶导数方程ƒ〞（x）＝0的根，……，直至满足其（m－1）阶导数方程ƒ（m－1）（x）＝0 的根，都含有原方程ƒ（x）＝0的根。

例如方程ƒ（x）＝x2＋3x＋2＝0有互异单根x1＝－1，x2＝－2，一阶导数方程ƒ′（x）＝2x＋3＝0 的根为x＝－3/2，ƒ′（x）＝0 的根不是原方程ƒ（x）＝0 的根。

方程ƒ（x）＝（x－1）（x－2）2＝0有二重根x1，2＝2，原方程的一阶导数方程ƒ′（x）＝（x－2）[（x－2）＋2（x－1）]＝0 的一个根x1＝2，仍然是原方程ƒ（x）＝0 的根。

方程ƒ（x）＝（x－1）（x－2）3＝0有三重根x1，2，3＝2，原方程的一阶导数方程ƒ′（x）＝（x－2）2[（x－2）＋3（x－1）]＝0的两个根x1，2＝2，仍然是原方程ƒ（x）＝0的根，原方程的二阶导数方程ƒ〞（x）＝（x－2）[（x－2）＋（x－1）]＝0的一个根x1＝2，仍然是原方程ƒ（x）＝（x－1）（x－2）2＝0 的根。

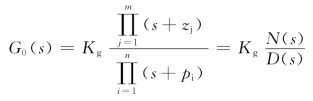
根据代数重根法则，可以计算根轨迹的分离点。系统的开环传递函数为其中N（s）为变量s 的分子多项式，最高次为m，D（s）为变量s 的分母多项式，最高次为n 。闭环特征方程可以写为

即

方程（4-21）的根即系统的闭环极点。根据代数重根法则，如果闭环极点为二重根，即分离点处为二重根则有

也是方程（4-21）的根，联立式（4-21）和式（4-22）可得分离点的计算公式为

由于系统的重根数目不会太多，一般只按照上式计算即可。另外，计算结果是否是分离点，还要作一下校验。如计算所得的值在实轴上，那么要判别该线段是否是根轨迹。如果该线段是根轨迹，则计算结果就是分离点。否则，不是分离点，要舍去。

（2）极值法。

由于函数ƒ（x）＝0 可以在重根处获得极值，因此由式（4-20）可以得到

(www.xing528.com)

则根轨迹增益Kg 为s 的函数。其极值计算公式为

得到

显然，式（4-26）和式（4-23）相同，即对Kg 求极值的方法和重根法所得的结果是一样的，Kg 具有极值和具有极值是一样的。因此式（4-26）也可写为

（3）试探法。

还可以用试探法来计算分离点坐标d，计算公式为

式中，m，n 分别为开环传递函数在实轴上零、极点数。关于公式的证明可以参阅其他参考教材。

图4-8绘出了4 支根轨迹在实轴上分离的情况。图4-9绘出了在复平面上有分离点的情况，复平面上的分离点是实轴对称的。

图4-8　四重根的分离点

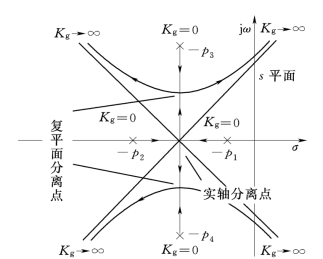
图4-9　复平面上分离点

法则5 根轨迹上的分离点和会合点的条件方程可由开环传递函数求得，即N′（s）D（s）－N（s）D′（s）＝0 的解，并须验证在实轴的分离点和会合点。

【例4-4】 设系统结构图与开环零、极点分布如图4-10所示，试绘制其概略根轨迹。

解：由法则1 可知，根轨迹有3 条分支，分别起始于（0，j0），（－2，j0），（－3，j0），一条终止于（－1，j0），另外两条止于无穷远处。

由法则2，根轨迹关于实轴对称。

由法则3，实轴上区域[0，－1]和[－2，－3]是根轨迹，在图4-10中以粗实线表示。

图4-10　例4-4 系统的结构图及其根轨迹图

（a）系统的结构图；（b）根轨迹图

由法则4，两条终于无穷的根轨迹的渐近线与实轴交角和交点坐标为

由法则5，N′（s）D（s）－N（s）D′（s）＝0，N（s）＝s＋1，D（s）＝s（s＋2）（s＋3），N′（s）D（s）－N（s）D′（s）＝s3＋4s2＋5s＋3＝0。

解这个高次方程可用试根法。因为分离点必在[－2，－3]区间，所以不妨试s＝－2.5，左侧为－0.125，右侧为零，再试s＝－2.47，两边近似相等。所以分离点坐标s ≈－2.47。

另用试探法求法如下：

实轴区域[－2，－3]必有一个根轨迹的分离点d，它满足下述分离点方程：

考虑到d 必在－2 和－3 之间，初步试探时，设d＝－2.5，算出

因方程两边不等，所以d＝－2.5 不是欲求的分离点坐标。现在重取d＝－2.47，方程两边近似相等，故本例d≈－2.47。最后画出的系统概略根轨迹，如图4-10（b）所示。