根轨迹的渐近线方程与实轴的交点和夹角

由法则1 可知，若n≥m，当Kg→∞，还有n－m 条根轨迹趋于s 平面的无穷远处。现在讨论它们以何种方式趋于无穷远处。由式（4-13）可得

式中，为负的零点之和，为负的极点之和。当Kg→∞时，由n≥m，有s→∞，上式可近似为

由于s→∞，将上式左边按牛顿二项式定理展开，近似取线性项（即略去高次项）则有

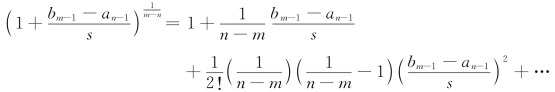
当s 很大时，

令

上式成为

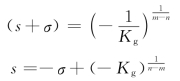
以－1＝ej180°（2k＋1），k＝0，1，2，…代入上式，则有

这是当s→∞时根轨迹的渐近线方程，它由两项组成。

第一项为实轴上的常数向量，为渐近线与实轴的交点，其坐标为(www.xing528.com)

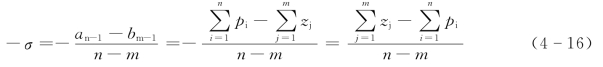
第二项为通过坐标原点的直线，与实轴的夹角（称为渐近线的倾斜角）为

式中，k＝0，1，2，…，由于相角的周期为360°，k 取到n－m－1 即可。

法则4 根轨迹的渐近线与实轴的夹角α和与实轴的交点σ0 由下式确定：

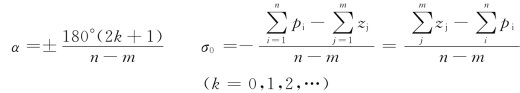
【例4-3】 已知控制系统的开环传递函数为

试确定根轨迹的分支数、起点和终点。若终点在无穷远处，试确定渐近线和实轴的交点及渐近线的倾斜角。

解：由于n＝3，所以有3 条根轨迹，起点分别在－P1＝0，－P2＝－1 和－P3＝－5。由于m＝0，开环传递函数没有有限值零点，所以三条根轨迹的终点都在无穷远处，其渐近线与实轴的交点σ0 及倾斜角α分别为

当k＝0 时，α1＝±60°；当k＝1 时，α2＝±180°；根轨迹的起点和三条渐近线如图4-6所示。

图4-6　根轨迹渐近线图