实轴根轨迹绘制法则及步骤

实轴上某一区域，若其右边开环实数零、极点的个数之和为奇数，则该区域必是根轨迹。

证明 设某一系统的开环零、极点分布如图4-4所示，若实轴上某一点是根轨迹上的点，它必满足相角方程式（4-12）。在实轴上任取一试验点s1，由图4-4可见，在复平面上任何一对共轭复数极点（或零点）到s1 处向量的相角之和为零，如图上而试验点s1 左侧实轴上的开环零、极点到s1 处向量的相角也为零，所以它们都不影响相角方程的成立。我们只需考虑试验点s1 右侧实轴上开环零、极点到s1 点处向量的相角，每个相角都为π，将上述关系代入相角方程式（4-12）中，则

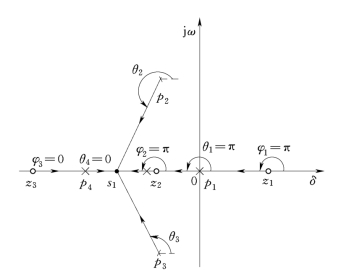
图4-4　实轴上的根轨迹

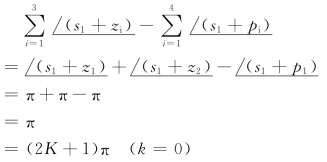
所以相角方程成立，即s1 是根轨迹上的点。而且s1 右侧有两个开环零点，一个开环极点，则它们数目之和为奇数。一般情况，设试验点右侧有l 个开环零点，h 个开环极点，则有关系式

若满足相角条件必有关系式

（l－h）π＝（2k＋1）π

所以，l－h 必为奇数，当然l＋h 也为奇数。(www.xing528.com)

法则3 实轴上的根轨迹完全由实轴上的开环极点和零点所确定，若某段实轴右侧的实极点数与实零点数之和是奇数，则这段实轴就是根轨迹的一部分；若某段实轴右侧的实极点数和实零点数之和为偶数，则它不是系统的根轨迹。

【例4-2】 设一单位负反馈系统的开环传递函数为G0（s）＝K（s＋1）/s（0.5s＋1），求K＝0→∞时闭环系统根轨迹。

解：将开环传递函数写成零、极点形式

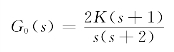
有一个开环零点，－z1＝－1。两个开环极点，－P1＝0，－P2＝－2。开环传递函数分子的阶数m＝1，分母的阶数n＝2。首先将开环零、极点布置在s 平面上，如图4-5所示，然后按绘制根轨迹的基本法则逐步画出根轨迹。

（1）由法则1 得有两条根轨迹，分别起始于开环极点0、2，一条终于有限零点－1，另一条趋于无穷远处。

（2）依据法则2，两条根轨迹对称于实轴且连续。

（3）依据法则3，在负实轴上，0 到－1 之间和－2 到负无穷区间是根轨迹。最后绘制出根轨迹如图4-5所示。

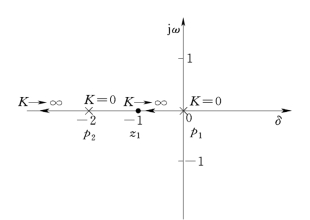
图4-5　例4-2 系统的根轨迹图