如何减小系统稳态误差？

（1）保证系统中各个环节，特别是反馈回路中元件的参数具有一定的精度和稳定性，必要时需采用误差补偿措施。

（2）增大系统开环增益或干扰输入作用位置前系统前向通道的环节所对应传递函数的增益，可以降低给定误差或扰动稳差。

（3）增加系统前向通道中积分环节的数目，可以提高系统的型号，从而消除不同输入作用时的稳差。但是，积分环节数目的增加会降低系统的稳定性，并影响到其他暂态性能指标。实际中，常用比例—积分微分控制器，效果会更好。

（4）采用前馈控制（复合控制），可以进行补偿。

补偿的方法是改善系统稳态精度的重要、全面、综合的方法。

系统的稳态误差主要是由积分环节的个数和放大系数来确定的。为了提高精度等级，可增加积分环节的数目，为了减小有限误差，可增加放大系数。但这样一来都会使系统的稳定性变差。而采用补偿的方法，则可在保证系统稳定的前提下减小稳态误差。

1.引入输入补偿

系统如图3-23所示，为了减小给定信号引起的稳态误差，从输入端引入一补偿环节Gr（s），这时系统的稳态误差为

图3-23　引入输入补偿的复合系统

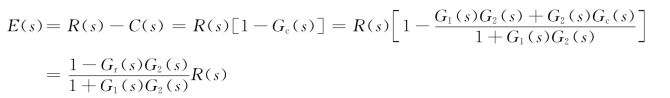
可见，若使1－Gr（s）G2（s）＝0，则(www.xing528.com)

就能实现所谓完全补偿，使系统的输出c（t）始终等于其输入r（t），无误差产生。由于补偿环节Gr（s）位于系统闭环回路之外，它对系统闭环传递函数的分母不会产生任何影响，即系统的闭环稳定性不会因它的加入而发生变化。

2.引入扰动补偿

系统如图3-24所示，为了减小扰动信号引起的误差，利用扰动信号经过Gr（s）来进行补偿。

图3-24　引入扰动补偿的复合系统

可见，要使E（s）＝0，必须满足

1＋Gn（s）G1（s）＝0

即取就可实现完全补偿。

在工程实践中，由于Gr（s）和Gn（s）物理实现上的原因，上述两种完全补偿的条件一般难于全部满足，而只能近似地实现。虽然在实践中采用的补偿是近似的，但它对改善系统的稳态性能仍产生十分有效的作用。

在负反馈控制的基础上，又引入补偿控制的系统称为复合控制系统。