如何计算稳态误差？

由于误差信号由稳态分量eS（t）和暂态分量et（t）组成，因此分别对稳态分量和暂态分量求t→∞时的极限，可得系统的稳差。即：

当t→∞时，暂态分量et（t）→0，即

当t→∞时，稳态分量eS（t）＝eSS，即

故稳态系统的误差（即稳差）为eSS。

对于同时受到给定输入作用和扰动输入作用的稳定系统，如图3-18所示，它的稳差eSS包含了给定输入作用r（t）引起的稳差分量eSSr和扰动输入作用n（t）引起的稳差分量eSSn，即eSS＝eSSr＋eSSn。

（1）若sER（s）、sEN（s）的极点全在左半复平面，则可应用Laplace 变换的终值定理分别求出eSSr、eSSn，然后可得eSS＝eSSr＋eSSn。

具体过程如下：

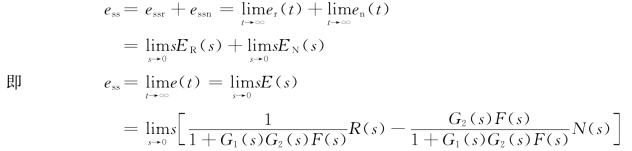
（2）若sER（s）、sEN（s）的极点不全在左半复平面，则可以把ER（s）、EN（s）经部分分式法化为若干个简单代数式的代数和，通过Laplace逆变换求得er（t）、en（t），再求t→∞时的极限可得eSSr、eSSn，从而可以得到eSS＝eSSr＋eSSn。

【例3-7】 如图3-20所示，已知，F（s）＝1，求：

1）r（t）＝10×1（t），n（t）＝1（t）；

2）r（t）＝1（t），n（t）＝Sin4t 时系统的稳差。

解：1）

因为sER（s）的极点全在左半复平面，所以有(www.xing528.com)

因为sEN（s）的极点全在左半复平面，所以有

因为sER（s）的极点全在左半复平面，所以有

因为sEN（s）的极点为－3，±j4；它们不全在左半复平面。

求eSSn时不能用Laplace变换的终值定理，而要将EN（s）通过部分分式法化为代数和形式，从而求得en（t），再求t→∞时的极限。

对于稳差，可以做出下列小结：

（1）稳定系统的误差传递函数的极点全在左半复平面，当外界输入作用（给定输入作用、干扰输入作用）为阶跃、斜坡、抛物线、脉冲函数时，sER（s）、sEN（s）的极点全在左半复平面（或不全在左半复平面，即在左半复平面和纯虚轴上）；此时，可以应用Laplace变换终值定理分别求出eSSr、eSSn，从而求出eSS。

（2）对于稳定系统，当外作用为典型谐波函数（正弦函数）时，不能套用Laplace 变换终值定理，只能通过ER（s）、EN（s）求Laplace 逆变换得到er（t）、en（t），然后取t→∞时的极限得到eSSr、eSSn，从而求出eSS。

对于复杂的系统，求解困难时，可以应用第五章的频域分析法，在频率特性函数的基础上求稳差。