【摘要】:如果无论怎样调整系统的参数,也无法使其稳定,则称这类系统为结构不稳定系统。图3-15结构不稳定系统结构图闭环传递函数为特征方程式为Ts3+s2+K=0根据劳斯判据,由于方程中s 一次项的系数为零,故无论K 取何值,该方程总是有根不在s 左半平面,即系统总是不稳定。这类系统称为结构不稳定系统。
如果无论怎样调整系统的参数,也无法使其稳定,则称这类系统为结构不稳定系统。如图3-15所示的系统。
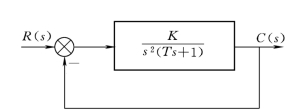
图3-15 结构不稳定系统结构图
闭环传递函数为
![]()
特征方程式为
Ts3+s2+K=0
根据劳斯判据,由于方程中s 一次项的系数为零,故无论K 取何值,该方程总是有根不在s 左半平面,即系统总是不稳定。这类系统称为结构不稳定系统。解决这个问题的办法一般有以下两种:
1.改变环节的积分性质
可用比例反馈来包围有积分作用的环节。例如,在积分环节外面加单位负反馈,见图3-16,这时,环节的传递函数变为
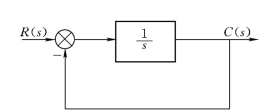
图3-16 积分环节外加单位负反馈
![]()
从而使原来的积分环节变成了惯性环节。图3-15所示系统中的一个积分环节加上单位负反馈后,系统开环传递函数变成为
![]()
系统的闭环传递函数为
![]()
特征方程式(https://www.xing528.com)
Ts3+(1+T)s2+s+K=0
劳斯表
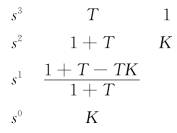
根据劳斯判据,系统稳定的条件为

所以,K 的取值范围为
![]()
可见,此时只要适当选取K 值就可使系统稳定。
2.加入比例微分环节
如图3-17所示,在前述结构不稳定系统的前向通道中加入比例微分环节,系统的闭环传递函数变为
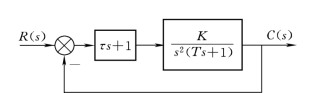
图3-17 系统中加入比例微分环节
![]()
劳斯表

系统的稳定条件为

可见,此时只要适当选取系统参数,便可使系统稳定。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




