二阶系统的性能评估指标优化

对欠阻尼二阶系统的性能指标进行讨论和计算。

欠阻尼二阶系统的单位阶跃响应曲线如图3-4所示。

1.上升时间tr

根据tr 的定义，有

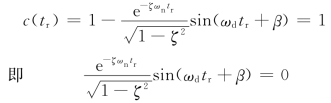
Sin（ωdtr＋β）＝0

ωdtr＋β＝0，π，2π，…

第一次达到稳态值有

其中

2.峰值时间tp

根据tp 的定义，可采用求极值的方法来求取。求导后，令该式为零，可以得到

3.超调量σ%

将代入欠阻尼二阶系统单位阶跃响应表达式，求得

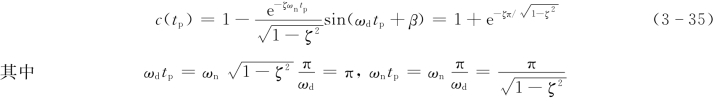
根据定义，由于c（∞）＝c（t）|t＝∞＝1 可得

(www.xing528.com)

4.调节时间tS

求取调节时间可用近似公式：

其中为系统的时间常数。当ζ大于上述值时，可采用近似公式计算

5.稳态误差eSS

根据稳态误差的定义和终值定理有

当阶跃输入时，由上式可算得eSS＝0。

以上为欠阻尼二阶系统在单位阶跃输入作用下性能指标的求取。对于过阻尼二阶系统，其性能指标只有调节时间tS 和稳态误差eSS。eSS 的计算同上。由于ζ≥1 时，系统的响应较慢，故二阶系统一般不设计成临界阻尼或过阻尼形式，只有在不允许出现超调的特殊要求下，才采用过阻尼形式。

当输入为单位斜坡信号，即时，可求得

由以上的分析可归纳出二阶系统性能分析要点：

（1）平稳性。主要由ζ决定，ζ↑→σ%↓平稳性越好。ζ＝0 时，系统等幅振荡，不能稳定工作。ζ一定时，ωn↑→ωd↑，系统平稳性变差。

（2）快速性。ωn 一定时，若ζ较小，则ζ↓→tS ↑，而当ζ＞0.7 之后又有ζ↑→tS↑。即ζ太小或太大，快速性均变差。

在控制工程中，ζ是由对超调量的要求来确定的。ζ一定时，ωn ↑→tS ↓。所以，要获得较好的快速性，阻尼比ζ不能太大，而ωn 可尽量选大。

综合考虑系统的平稳性和快速性，一般将ζ＝0.707 称为最佳阻尼比，此时，系统不仅响应速度快，而且其超调量较小（σ%＝4.3%）。对应的二阶系统称为最佳二阶系统。

（3）准确性。ζ的增加和ωn 的减小虽然对系统的平稳性有利，但将使得系统跟踪斜坡信号的稳态误差增加。