【摘要】：相应的单位阶跃响应的形式也不相同。输出响应的拉氏反变换此时，系统输出随时间t 单调上升，无振荡和超调，由于输出响应含负指数项，因而随着时间推移，对应的分量逐渐趋于零，输出响应最终趋于稳态值。图3-9欠阻尼二阶系统参数间的关系则欠阻尼二阶系统的单位阶跃响应可写成系统的响应为衰减振荡波形，系统有超调。输出的拉氏变换为其拉氏反变换为系统的单位阶跃响应为等幅振荡波形。图3-10为取不同ζ值时对应的单位阶跃响应曲线。
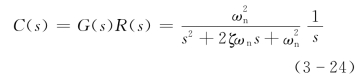
其中，由s2＋2ζωns＋ω2n＝0 可求得两个特征根，即
对不同的ζ值，s1，s2 的性质是不同的，即s1，s2 有可能为实数根、复数根或重根。相应的单位阶跃响应的形式也不相同。
1.ζ＞1 过阻尼振荡状态
特征根
，为两个不相等的负实数根，即有
其中，A1、A2、A3 为待定数。
输出响应的拉氏反变换
此时，系统输出随时间t 单调上升，无振荡和超调，由于输出响应含负指数项，因而随着时间推移，对应的分量逐渐趋于零，输出响应最终趋于稳态值。
2.ζ＝1 临界阻尼振荡状态
特征根s1，2＝－ζωn＝－ωn，有一对重负实根。
输出的拉氏变换为
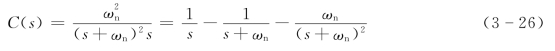
拉氏反变换得
响应曲线输出无振荡和超调。系统的响应速度在ζ＝1 时比ζ＞1 时快。
3.0＜ζ＜1 欠阻尼振荡状态
特征根
令阻尼振荡频率
(https://www.xing528.com)
则s1，2＝－ζωn±jωd，为一对复数根。
输出的拉氏变换为
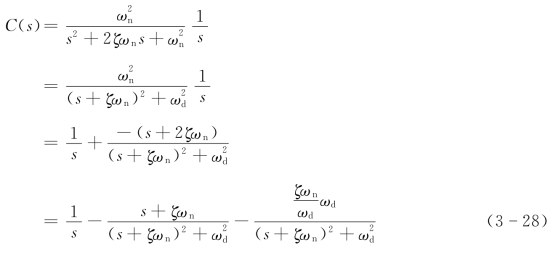
取拉氏反变换得
将上式整理为
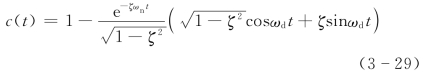
设欠阻尼二阶系统参数之间的关系为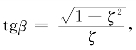
，如图3-9所示。
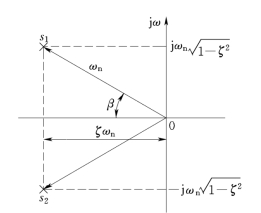
图3-9 欠阻尼二阶系统参数间的关系
则欠阻尼二阶系统的单位阶跃响应可写成
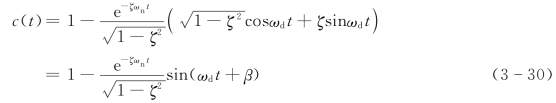
系统的响应为衰减振荡波形，系统有超调。
4.ζ＝0 无阻尼振荡状态
特征根s1，2＝±jωn 为一对纯虚根。
输出的拉氏变换为
其拉氏反变换为
系统的单位阶跃响应为等幅振荡波形。
图3-10为取不同ζ值时对应的单位阶跃响应曲线。由图可见，ζ值越大，系统的平稳性越好，超调越小；ζ值越小，输出响应振荡越强，振荡频率越高。当ζ＝0 时，系统输出为等幅振荡，不能正常工作，属不稳定。
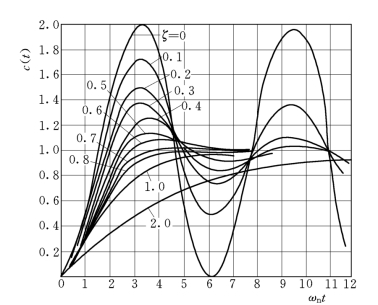
图3-10 不同ζ值时系统的单位阶跃响应
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
