根据图2-37可以求出系统的传递函数,这涉及到动态结构图的化简问题。

图2-37 位置随动系统动态结构图
(一)等效变换原则
结构图化简需要遵循一定的基本原则,也就是要保证化简前后的代数等价关系不变。
1.环节串联
串联环节的传递函数等于各串联环节传递函数的乘积,如图2-38所示。由图可见,环节串联的结果是,两个方块合并成为一个方块,减少了方块的个数。

图2-38 环节串联化简
2.环节并联
并联环节的传递函数等于各并联环节传递函数的代数和,如图2-39所示。由图可见,环节并联化简的结果是,两条通路合并成为一条通路,减少了通路的条数。
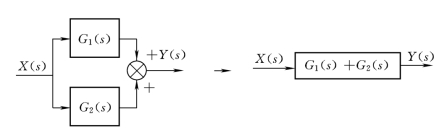
图2-39 环节并联化简
3.反馈回路
反馈回路如图2-40所示,可以将带有反馈回路的结构图简化成为一个方块。
![]()
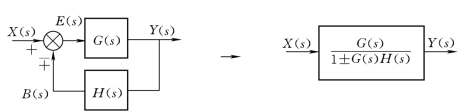
图2-40 反馈回路化简
式中,正号为负反馈,负号为正反馈。若H(s)=1,为单位反馈。
证明:设中间变量B(s),E(s)如图,则有
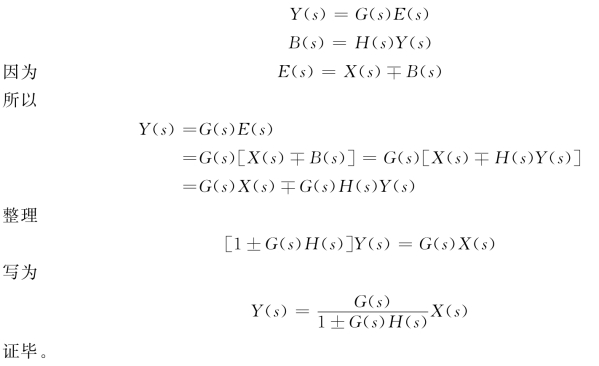
对于反馈回路,我们把![]() 又称为系统的闭环传递函数。把G(s)H(s)=G0(s),称为闭环系统的开环传递函数,也就是指从反馈环节H(s)末端断开时,系统前问通路传递函数G(s)与反馈通路传递函数H(s)的乘积。
又称为系统的闭环传递函数。把G(s)H(s)=G0(s),称为闭环系统的开环传递函数,也就是指从反馈环节H(s)末端断开时,系统前问通路传递函数G(s)与反馈通路传递函数H(s)的乘积。
4.相加点移动
相加点也就是求和点,将位于方块输入端(或者输出端)的相加点移动到方块的输出端(或者输入端),逆移、顺移与互易规则如图2-41~图2-43所示。这里的“逆移”、“顺移”指相加点逆着或顺着信号传递的箭头方向移动。
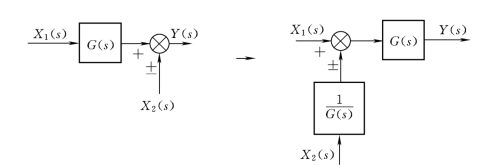
图2-41 相加点逆移
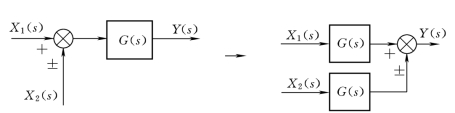
图2-42 相加点顺移
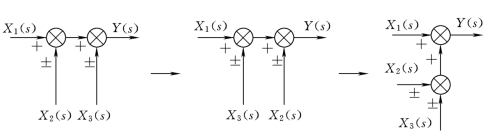
图2-43 相加点互易
5.分支点移动
分支点逆移如图2-44所示。分支点顺移如图2-45所示。
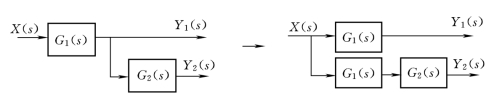
图2-44 分支点逆移
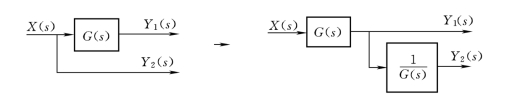
图2-45 分支点顺移
注意:相加点与分支点之间没有简单互易法则。
从以上分析可以看出,相加点逆移时,为保证等效应在移动支路中除以跨越的传递函数;相加点顺移时,为保证等效应在移动支路中乘以跨越的传递函数;分支点逆移时,为保证等效应在移动支路中乘以跨越的传递函数;分支点顺移时,为保证等效应在移动支路中除以跨越的传递函数。为了方便记忆,不妨记忆其中的三个字:“加、顺、乘”,“加”和“分”相对,“顺”和“逆”相对,“乘”和“除”相对。三者中必有也只有两个字能变。如“加逆除”,“分顺除”等。
【例2-20】 两级RC 滤波网络的结构图如图2-46(a)所示,试采用结构图等价变换法则化简结构图。
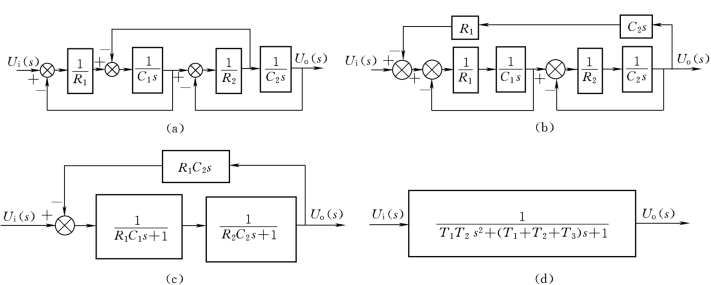
图2-46 两级RC 网络的结构图
解:由结构图可见,该图只有一条前向通路,三个反馈支路,也就是有三个自闭合回路,但回路中信号并不独立,回路内部有信号的相加点或分支点。所以在结构图分析时,首先将回路内部的相加点与分支点移出环外,就可以利用化简公式了。
第一步:逆箭头方向移出相加点,顺箭头方向移出分支点如图2-46(b)所示。
第二步:化简两个内部回路,并合并反馈支路中的串联环节如图2-46(c)所示。
第三步:T1=R1C1,T2=R2C2,T3=R1C2,作反馈回路化简如图2-46(d)所示。
所以,得到该网络的传递函数为
![]()
几种基本的结构图等效变换法则列于表2-3中。
表2-3 结构图等效变换法则
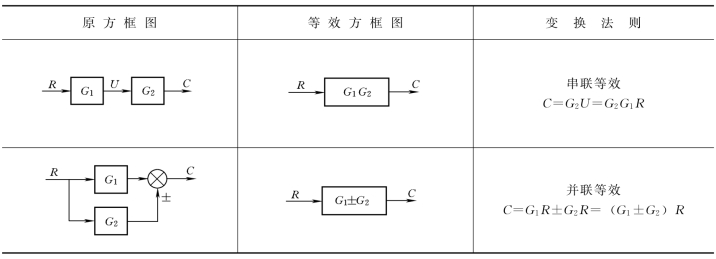
续表
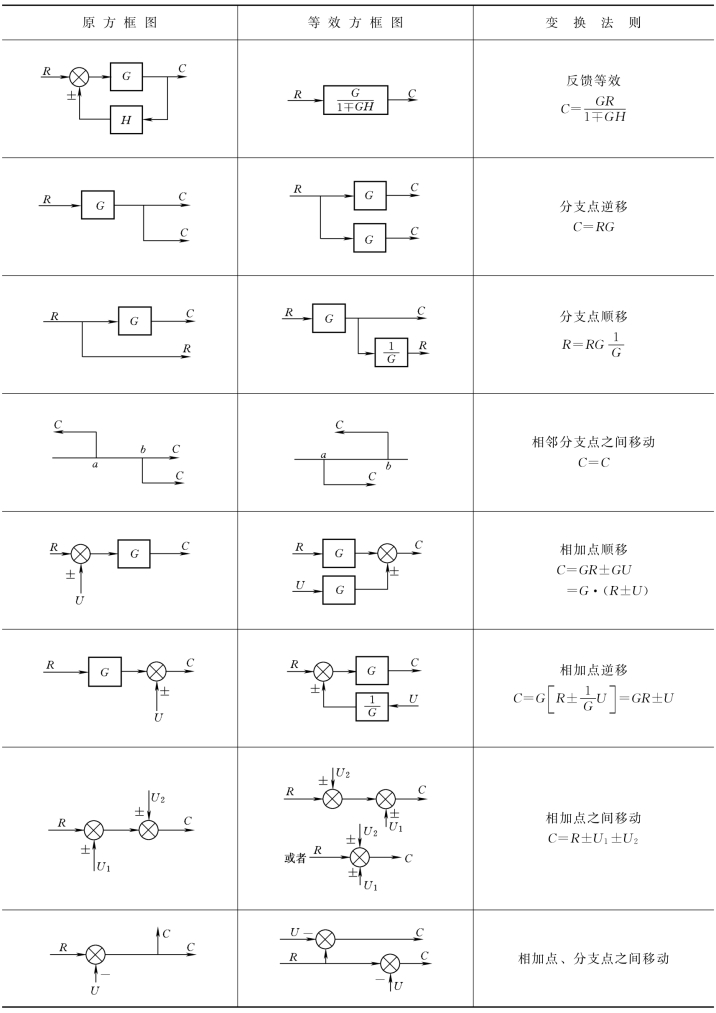
掌握了上述几种结构图等效变换法则后,对于一般的较复杂的结构图都能等效地变成典型的连接,求出其传递函数。但是,有时更复杂的结构图,只用上面变换法则还不能简化,例如,在结构图中有相加点分支点相间存在,为了简化结构图就要使它们之间互相移位,这种问题就要具体分析,不过仍然遵循着变换后信号传递关系不变的原则,如图2-47(a)所示。相加点、分支点在图中的位置是相间存在的,若变成典型结构连接,用前面介绍的几种原则都不适用,只能首先根据信号传递关系,将结构图重新排列,变相加点分支点相间为相邻,从而达到简化目的,如图2-47(b)所示。
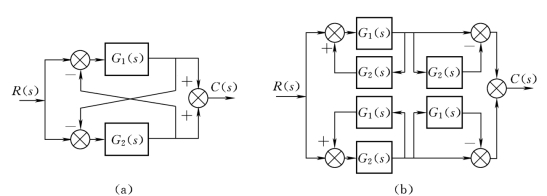
图2-47 相加点和分支点之间移位的等效变换
(二)梅森(S.J.MaSon)公式
根据结构图等效化简原则,将结构图化成最简方框图,可以求得系统的传递函数。但是化简步骤仍然需要一步一步进行。而采用梅森公式化简结构图,求得系统的传递函数,只需要做少量的计算,就可以将传递函数一次写出。所以是一种简捷方便的求法。
梅森公式是基于信号流图理论的一套计算公式,用于计算线图的总增益。结构图与信号流图有密切的关系。
1.信号流图中的基本概念
(1)节点:表示变量。如x1,x2,…。节点自左向右顺序设置,每个节点标志的变量是所有流向该节点的信号的代数和,而从同一节点流向各支路的信号均用该节点的变量表示。
(2)源节点(输入节点):在该节点上,只有信号的输出支路,没有信号的输入支路。它一般代表系统的输入变量,故也称输入节点。如图2-48中的x1 节点。
(3)阱节点(输出节点):在该节点上,只有信号的输入支路而没有输出支路,它一般代表系统的输出变量,故也称输出节点,如图2-48中的x6 节点。
(4)混合节点:在该节点上,既有信号的输入支路又有输出支路。如图2-48中的x2 节点。(https://www.xing528.com)
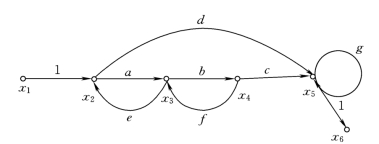
图2-48 典型的信号流图
(5)支路:两节点之间的定向线段。如图2-48中的x2→x3。
(6)支路增益:两变量间的增益(即两变量间的传递函数)。如图2-48中的x2→x3支路增益为a。
(7)通路:沿支路箭头方向穿过各相连支路的途径。如图2-48中的x2→x3→x4→x5 节点。
(8)前向通路:从输入节点到输出节点的通路上,通过任何节点不多于一次,则该通路称为前向通路。如图2-48中有两条前向通路,一条是x1→x2→x3→x4→x5→x6,另一条是x1→x2→x5→x6。
(9)前向通路增益:前向通路中,各支路的增益的乘积称为前向通路增益(包括正负号)。一般用Pk 表示,如图2-48中的P1=1abc1;P2=ldl。
(10)回路:若通路的终点就是通路的起点,并且与其他任何节点相交不多于一次的通路就称为回路。如图2-48中的x2→x3→x2;x3→x4→x3;x5→x5 等。
(11)回路增益:回路中各支路的增益乘积,称为回路增益(包括正负号)。如图2-48中的L1=ae;L2=bƒ;L3=g 等。
(12)不接触回路:若一些回路之间没有任何公共点就称这些回路为不接触回路。如图2-48中有两组不接触回路,一组是x2→x3→x2 和x5→x5;另一组是x3→x4→x3 和x5→x5。
2.结构图和信号流图
从图2-49可以看到,支路、支路增益、回路等,两图是一一对应的,所以应用梅森公式做结构图化简时,可以省去信号流图,直接在结构图上完成。

图2-49 结构图和信号流图
(a)系统的结构图;(b)信号流图
3.梅森公式
梅森总增益计算公式描述如下

式中 P——系统的总增益(总的传递函数);
Pi——从输入到输出的第i 条前向通路的增益;
Δ——梅森公式的特征式;
Δi——第i 条前向通路的余子式。
梅森公式的特征式的计算公式是
![]()
式中![]() ——所有独立回路增益之和;
——所有独立回路增益之和;
![]() ——所有两两互不接触回路增益乘积之和;
——所有两两互不接触回路增益乘积之和;
![]() ——所有三三互不接触回路增益乘积之和。
——所有三三互不接触回路增益乘积之和。
梅森公式中第i 条前向通路的余子式计算公式为:在特征式Δ中,将与第i 条前向通路Pi 相接触的回路各项全部去除后剩下的余子式即为Δi。
【例2-21】 两级RC 网络的结构图如图2-50所示,试用梅森公式求系统的传递函数。
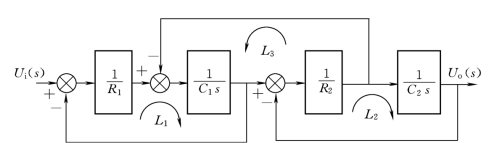
图2-50 两级RC 网络的结构图
解:(1)找出所有的前向通路并求其增益。系统共有一条前向通路,即
![]()
(2)写出所有独立回路,共3 个,即
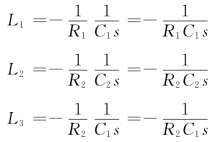
(3)找出两两互不接触回路,求出![]() ,以及找出三三互不接触回路,求出
,以及找出三三互不接触回路,求出![]() ,…依此类推。
,…依此类推。
本系统中只有一组两两互不接触回路,![]()
(4)写出梅森公式特征式Δ,即
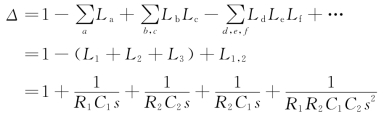
(5)写出各前向通路的余子式。因为只有一条前向通路,而回路1,2,3 都与之有接触,在特征式Δ中去除回路1,2,3 中的各项,则Δ1=1。
(6)系统传递函数为
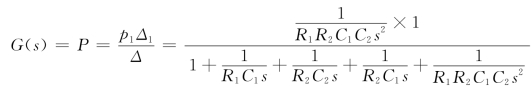
![]()
【例2-22】 三级RC 滤波网络如图2-51所示,试用梅森公式求取系统的传递函数。
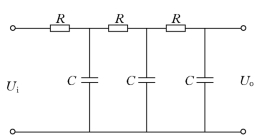
图2-51 三级RC 网络
解:三级RC 网络结构图如图2-52所示。
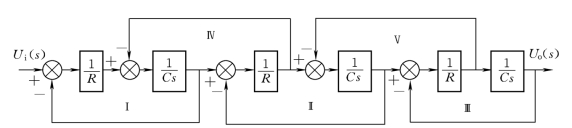
图2-52 三级RC 网络结构图
(1)一条前向通路
![]()
(2)5 个独立回路
![]()
(3)两两互不接触回路有6 组
![]()
(4)三三互不接触回路有一组
![]()
(5)特征式
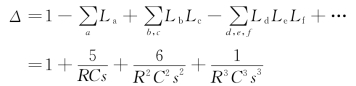
(6)余子式,各回路与前向通路均有接触,所以Δ1=1。
(7)传递函数
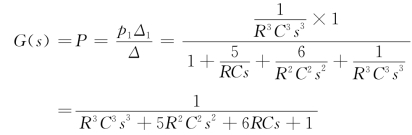
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




