典型元部件的传递函数解析

控制系统是由各种元部件组成的，它们可以是电子的、机械的、液压的、气动的等等。为了求得整个系统的传递函数，首先必须求得各个元部件的传递函数。这里介绍几种常见的元部件传递函数，根据实际需要可以查有关资料。

1.电位器

电位器是把角位移或线位移变成电压信号的装置，如图2-23所示。

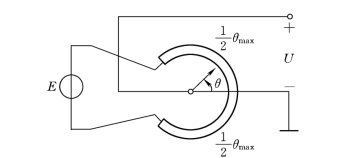
图2-23　电位器

在空载时，电位器的转角θ（t）与输出电压u（t）的关系是：

式中 E——电源电压，V；

θmax——电位器最大工作角度，rad；

K1——电位器传递系数，V/rad。

对式（2-102）进行拉氏变换，可得其传递函数为

电位器方框图如图2-24所示。

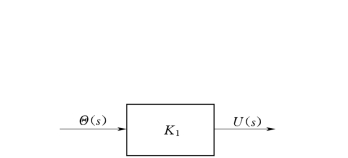
图2-24　电位器方框图

2.电位器电桥

电位器电桥是由两个相同电位器组成的误差信号检测器，如图2-25所示。

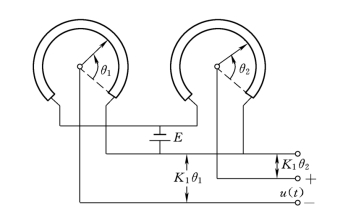
图2-25　电位器电桥

电位器电桥的输出电压为

式中 K1——单个电位器传递系数，V/rad；

Δθ——误差角，rad，Δθ＝θ1（t）－θ2（t）。

对式（2-104）进行拉氏变换，得电位器电桥的传递函数为电位器电桥的方框图如图2-26所示。

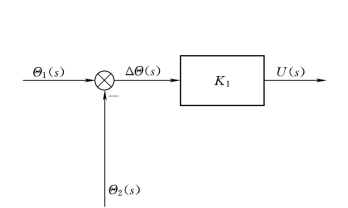
图2-26　电位器电桥方框图

单个电位器或电位器电桥，在空载时，从上面输入、输出关系推导中可知是线性元件，但是，在实际应用中都要与负载相连，这时负载对输出特性将产生影响，这就是负载效应问题，如图2-27所示电路。

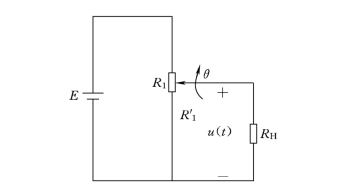
图2-27　负载效应

图中R1 为电位器电阻，RH 为负载电阻，这时电位器的输出电压u（t）为

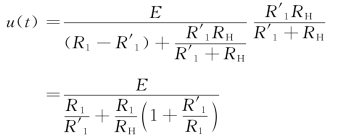
由于，将其代入上式，则

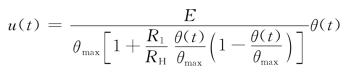
由上式可见，由于有了负载电阻RH，电位器的输出、输入关系不再是线性关系了，也就求不出传递函数了。只有当RH≫R1 时（一般取RH≥10R1），u（t）＝K1θ（t）关系式才成立。

3.无源网络

为了改善系统的性能，在系统中引入无源网络作为校正元件。无源网络通常由电阻、电容、电感组成，利用电路理论可方便地求出其动态方程，对其进行拉氏变换求出传递函数。这里需要说明，求无源网络的传递函数可以不通过求动态方程、拉氏变换的方法，而直接用复数阻抗来求。电阻、电容、电感的复数阻抗分别为R、1/Cs、Ls，它们的串、并联运算关系类同电阻。例如，前面提到的RC 无源网络，如图2-28所示。如用复数阻抗输出输入的关系式为

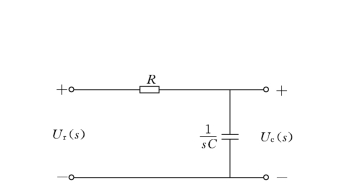
图2-28　RC 无源网络复数阻抗表示形式(www.xing528.com)

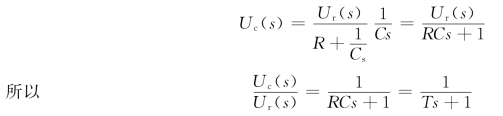
显然，这种方法求传递函数比用拉氏变换方法简单。

另外，求无源网络传递函数时也要注意负载效应。一般认为负载阻抗是无穷大的，这是考虑到无源网络在系统中处在运算放大器之前，否则要考虑负载效应。

4.测速发电机

测速发电机是将角速度信号转换成电压信号的测速装置，在机电伺服系统中常用它来作为局部反馈元件。测速发电机有交流、直流之分，如图2-29所示。

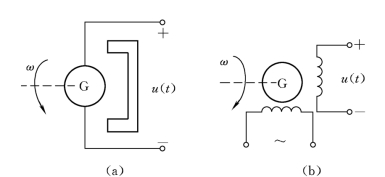
图2-29　测速发电机

（a）直流测速发电机；（b）交流测速发电机

永磁式直流测速发电机的转子与待测轴相连，输出与转子转轴角速度成正比的电压信号。交流发电机有两个互相垂直放置的线圈，一个是激磁绕组，接入一定频率的正弦额定电压信号，另一个为输出绕组，当转子旋转时，输出绕组产生与转子轴转速成比例的交流电压信号，其频率与激磁电压频率相同，如输出电压的包络用u（t）表示，则两种电机输出、输入关系都可以表示为

传递函数为

或

式中 u（t）——输出电压信号，V；

θ（t）——电机转子轴角位移，rad；

ω（t）——电机转子轴角速度，rad·S－1；

Kt——测速发电机输出斜率，V/（rad·S－1）。

测速发电机方框图如图2-30所示。

图2-30　测速发电机的方框图

5.电枢控制他激直流伺服电动机

电枢控制他激直流伺服电动机广泛用在控制系统中作为执行元件，驱动被控对象运动。其微分方程如式（2-1），传递函数为

电枢控制他激直流伺服电动机方框图如图2-31所示。

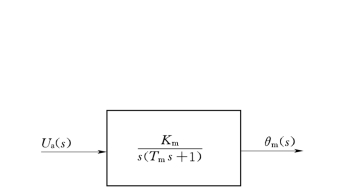
图2-31　电枢控制他激直流伺服电动机方框图

6.齿轮系

在控制系统中，伺服电动机与负载轴之间往往通过齿轮系进行传动，以实现减速和增大力矩的目的，其结构如图2-32所示。

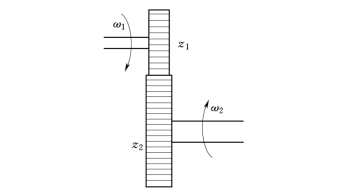
图2-32　齿轮系

图中z1，ω1 为主动齿轮的齿数和转速，z2 和ω2 为从动齿轮的齿数和转速。一级齿轮传动比为

如果有n－1 级传动，显然总的传动比为

式中ij（j＝1，2，…，n－1）为第j 级齿轮传动比。若增速传动i＜1，减速传动i＞1，在控制系统中一般用作减速传动。这时传递函数为

从式（2-112）看出齿轮系的传递函数是传动比的倒数。此系统中没有考虑负载的影响，当考虑通过一级齿轮连接负载时，一般要将负载的转动惯量、粘性摩擦系数折算到电动机轴上，这里不再详述。