拉氏变换基本定理总结

1.线性定理

若函数ƒ1（t），ƒ2（t）的拉氏变换分别为F1（s），F2（s），则

2.延迟定理

若函数ƒ（t）的拉氏变换为F（s），则

信号ƒ（t）与它在时间轴上的平移信号ƒ（t－τ）的关系如图2-17所示。

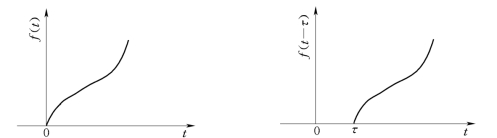
图2-17　信号的时间延迟示意图

该定理说明了时间域的平移变换在复数域有相对应的衰减变换。

应用延迟定理，可以简化一些信号的拉氏变换的求取。

【例2-9】 周期锯齿波信号如图2-18所示，试求该信号的拉氏变换。

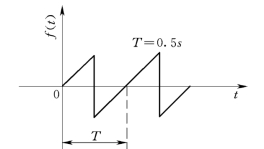
图2-18　锯齿波信号

解：该信号为周期信号。因此，已知信号第一周期的拉氏变换为F1（s）时，应用拉氏变换的延迟定理，得到周期信号的拉氏变换为

锯齿波信号第一周期的拉氏变换为

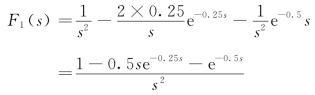
所以，锯齿波信号的拉氏变换为

3.衰减定理

若函数ƒ（t）的拉氏变换为F（s），则

该定理说明了时间信号ƒ（t）在时间域的指数衰减，其拉氏变换在变换域就成为坐标平移。当时间函数带有指数项因子时，利用拉氏变换的衰减定理，可以简化其拉氏变换的求取计算。

【例2-10】 试求时间函数ƒ（t）＝e－αt Sinωt 的拉氏变换。

解：因为正弦函数的拉氏变换为

所以，应用拉氏变换的衰减定理可以直接写出

另外，衰减定理与延迟定理也表明了时间域与变换域的对偶关系。

4.微分定理

若函数ƒ（t）的拉氏变换为F（s），且ƒ（t）的各阶导数存在，则ƒ（t）各阶导数的拉氏变换为

当所有的初值（各阶导数的初值）均为零时，即

则

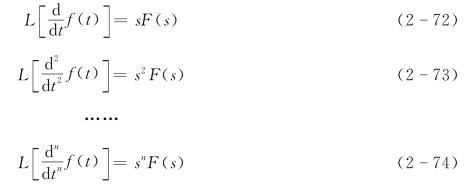
证明：（在此只证明一阶导数的拉氏变换，其余请读者自证）

由拉氏变换的定义式

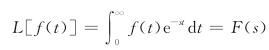
利用分部积分公式

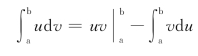
令

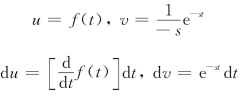
则(www.xing528.com)

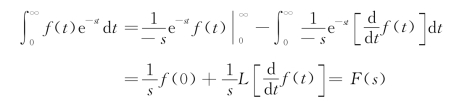
所以

证毕。

5.积分定理

若函数ƒ（t）的拉氏变换为F（s），则

定理的证明同样采用分部积分公式可以证得，请读者自证。式中

为函数ƒ（t）的在t＝0 时刻的积分值。

积分定理与微分定理互为逆定理。

6.初值定理

若函数ƒ（t）拉氏变换为F（s），且在t＝0＋处有初值ƒ（0＋），则

即时域函数的初值，可以由变换域求得。

证明：由微分定理令s→∞即可证得。

注意，拉氏变换的初值定理是满足拉氏变换的定义的，因此由初值定理所求得的时间信号的初值为ƒ（0＋），而不是ƒ（0）或者ƒ（0－）。例如阶跃信号1（t），可以利用拉氏变换的初值定理求得其初值为

7.终值定理

若函数ƒ（t）的拉氏变换为F（s），且ƒ（∞）存在，则

即时域函数的终值，也可以由变换域求得。

证明：由微分定理

两边对s→0 取极限

因为，所以方程左边

方程右边

所以

证毕。

8.卷积定理

若时域函数ƒ1（t），ƒ2（t）分别有拉氏变换F1（s），F2（s），时域函数的卷积积分为

又常表示为

则其拉氏变换为

这表明时域函数卷积积分在变换域成为变换域函数的乘积。证明可参考其他教材。

时域函数在变换域中表示有两个优点。一个优点是简化了函数，例如指数函数和正、余弦函数都是时域中的超越函数，在变换域中成为有理函数表示；另一个优点是简化了运算，如时域函数的卷积积分在变换域中成为变换域函数的乘积。

常用的拉氏变换基本定理可以参见表2-2。

表2-2　拉普拉斯变换的基本性质表