常用信号的拉氏变换

系统分析中常用的时域信号有脉冲信号、阶跃信号、正弦信号等。现说明一些基本时域信号拉氏变换的求取。

1.单位脉冲信号

理想单位脉冲信号的数学表达式为

说明：

单位脉冲函数可以通过极限方法得到。设单个方波脉冲如图2-13所示，脉冲的宽度为a，脉冲的高度为，面积为1。当保持面积不变，方波脉冲的宽度a 趋于无穷小时，高度趋于无穷大，单个方波脉冲演变成理想的单位脉冲函数。在坐标图上经常将单位脉冲函数δ（t）表示成单位高度的带有箭头的线段。

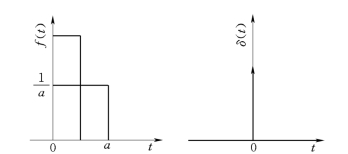
图2-13　单位脉冲函数

由单位脉冲函数δ（t）的定义可知，其面积积分的上下限是从0－到0＋的。因此在求它的拉氏变换时，拉氏变换的积分下限也必须是0－。由此，特别指明拉氏变换定义式中的积分下限是0－，是有实际意义的。所以，拉氏变换的积分下限根据应用的实际情况有0－，0，0＋三种情况。为不丢掉信号中位于t＝0 处可能存在的脉冲函数，积分下限应该为0－。

2.单位阶跃信号

单位阶跃信号的数学表示为

又经常写为

由拉氏变换的定义式，求得拉氏变换为

因为

阶跃信号的导数在t＝0 处有脉冲函数存在，所以单位阶跃信号的拉氏变换，其积分下限也规定为0－。单位阶跃信号如图2-14所示。

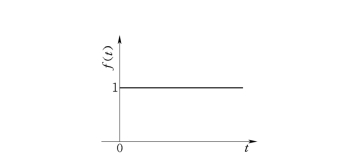
图2-14　单位阶跃信号

3.单位斜坡信号

单位斜坡信号如图2-15所示。单位斜坡信号的数学表示为

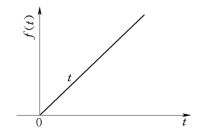
图2-15　单位斜坡信号

另外，为了表示信号的起始时刻，有时也经常写为(www.xing528.com)

为了得到单位斜坡信号的拉氏变换，利用分部积分公式

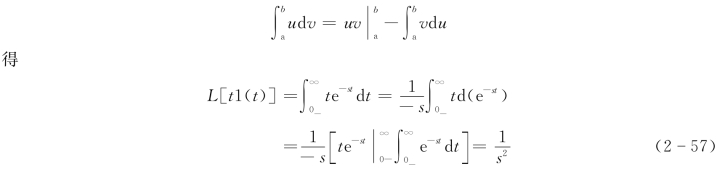
4.指数信号

指数信号如图2-16所示。指数信号的数学表示为

图2-16　指数信号

拉氏变换为

5.正弦、余弦信号

正弦、余弦信号的拉氏变换可以利用指数信号的拉氏变换求得。由指数函数的拉氏变换，可以直接写出复指数函数的拉氏变换为

因为

由欧拉公式

有

分别取复指数函数的实部变换与虚部变换，则有正弦信号的拉氏变换为

同时，余弦信号的拉氏变换为

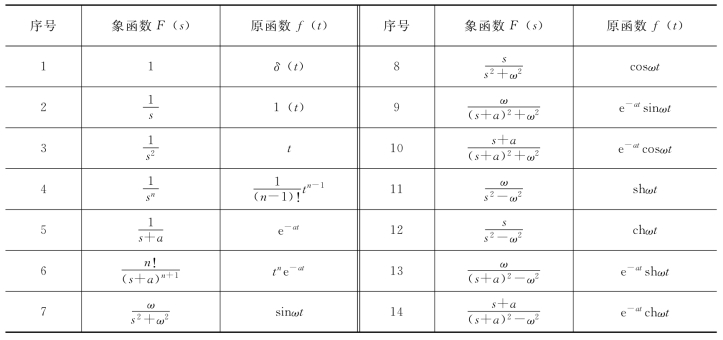
常见时间信号的拉氏变换可以参见表2-1。

表2-1　常见函数的拉普拉斯变换表