带R-L负荷的单相半波二极管整流器如图5-2a所示,各电路波形如图5-2b~d所示。
可以看出,负荷电流不仅在电源电压的正半周存在,负半周的一部分也有负荷电流[6]。存储了能量的负荷电感可以维持负荷电流,电感的端电压会克服负向电源,使二极管保持正向偏压和导通状态。图5-2c中,A区和B区面积相同。当二极管导通时,下列公式成立:

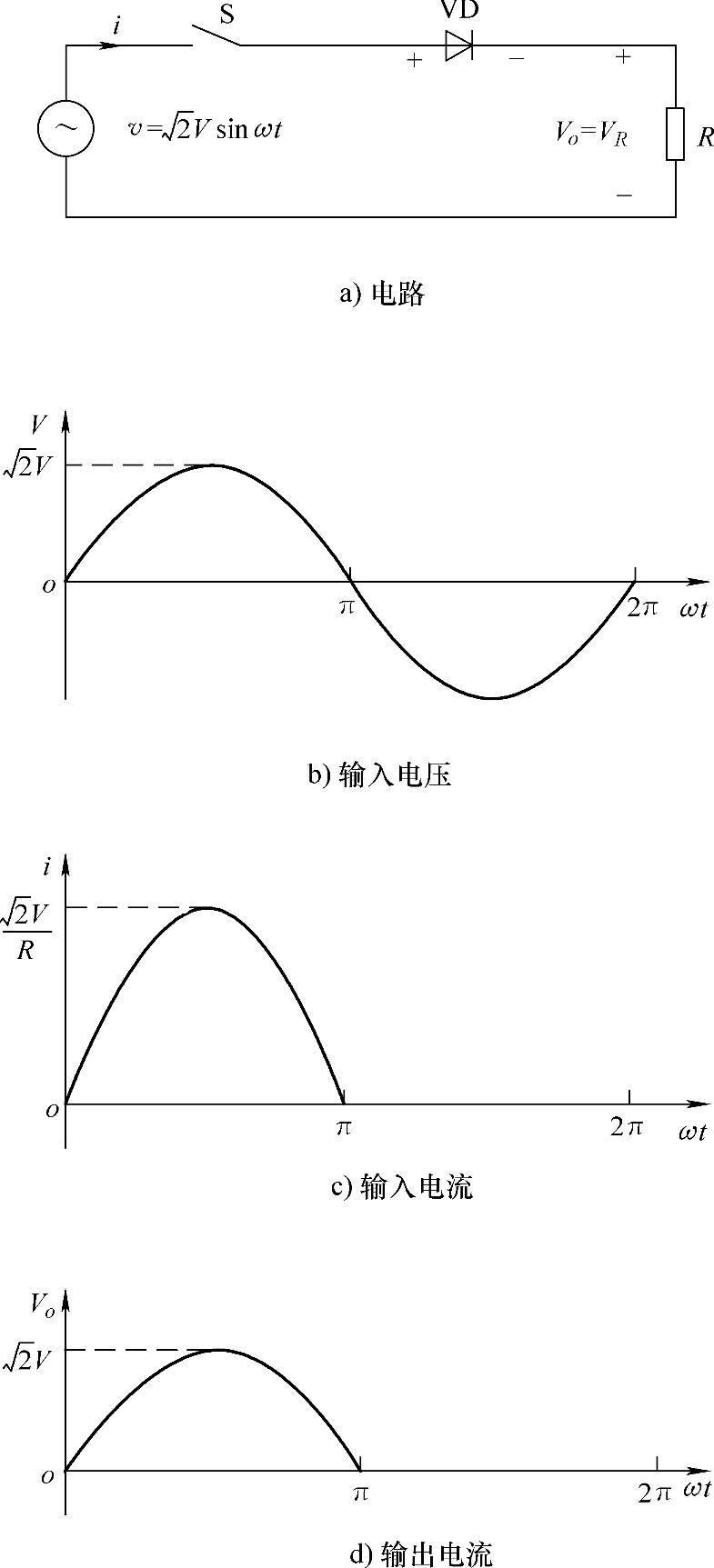
图5-1 R负荷SPHW二极管整流器
即
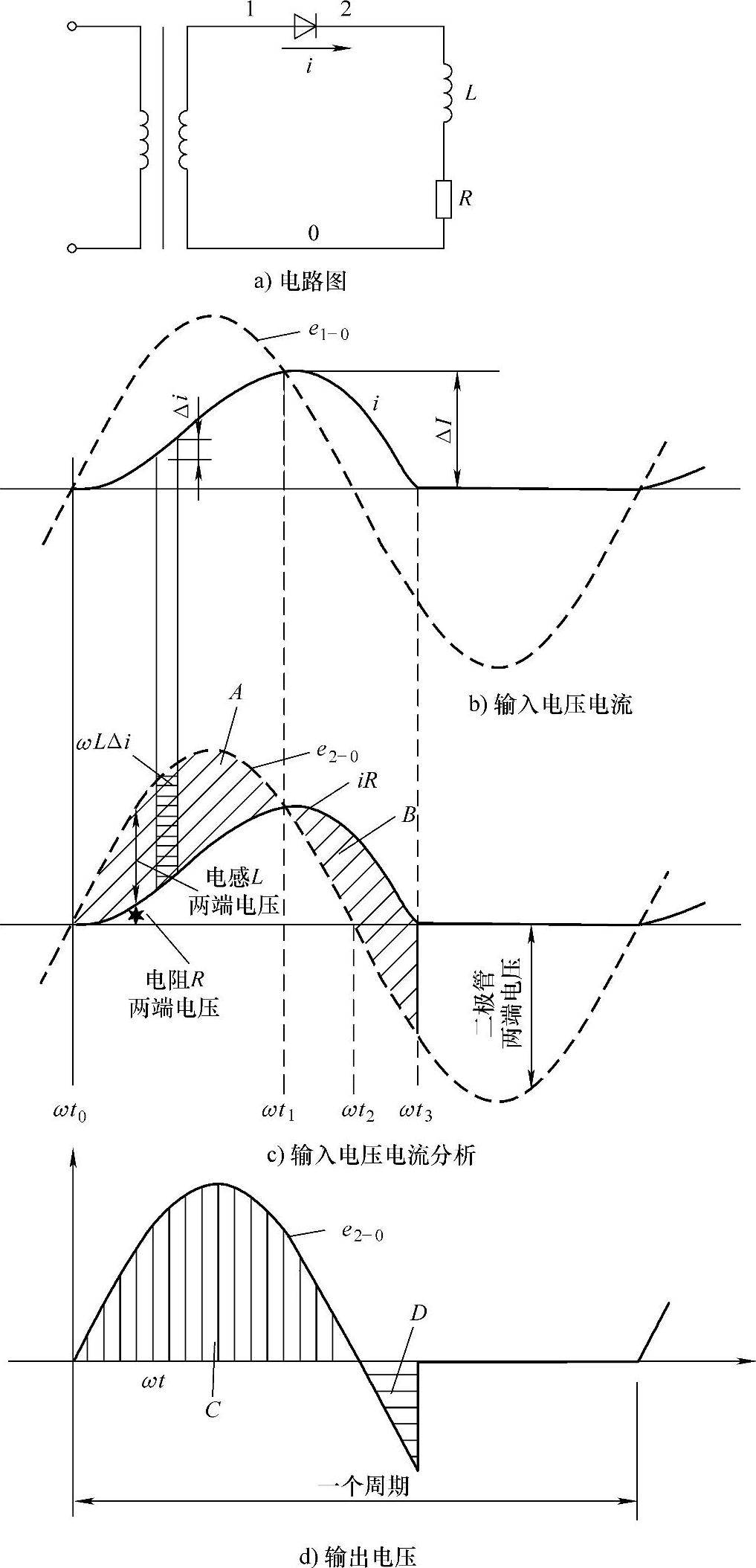
图5-2 R-L负荷单相半波整流器
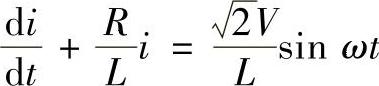
这是一个非规范的微分方程。它的解包括两部分,其强制分量为
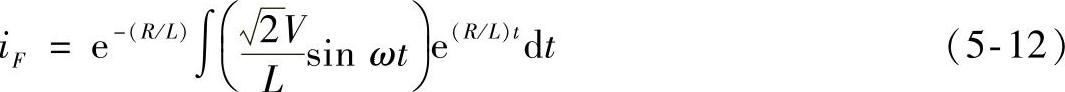
如果电路在负半周闭锁,则通过正弦稳态电路分析得到的电流强制分量为

式中

电路的固有响应为
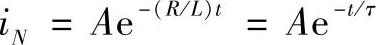 其中
其中 
因此
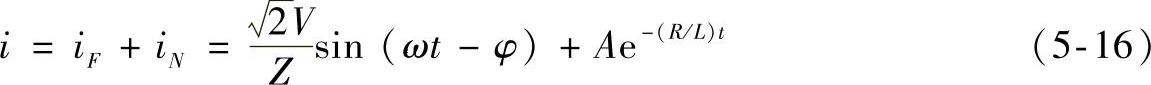
式中

把t=0时的初始条件i=0带入式(5-16),可得到常数A为
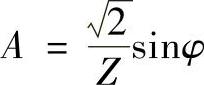
因此
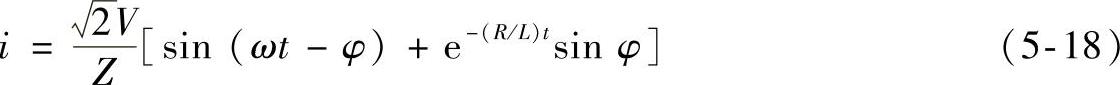
定义电流值为零时的β值为熄弧角,因此
i=0,β≤ωt<2π (5-19)
电流熄弧角β由负荷阻抗决定,在i=0、ωt=β时,可以用式(5-18)求得[1],即
sin(β-φ)=-e-Rβ/ωLsinφ (5-20)
这是一个关于未知数值β的超越方程,见图5-3。sin(β-φ)是正弦函数,e-Rβ/ωL sinφ是指数衰减函数。这两个函数的交点即β的工作点。
β值可使用MATLAB仿真获取,也可以用迭代法等数值法求解。
(1)图形法
用MATLAB解方程式(5-20),图5-4绘出了不同φ值时相应的β值。图中可以看到,β[X]轴从180°开始,在φ值较小时呈现线性特征,近似于
β≈π+φ
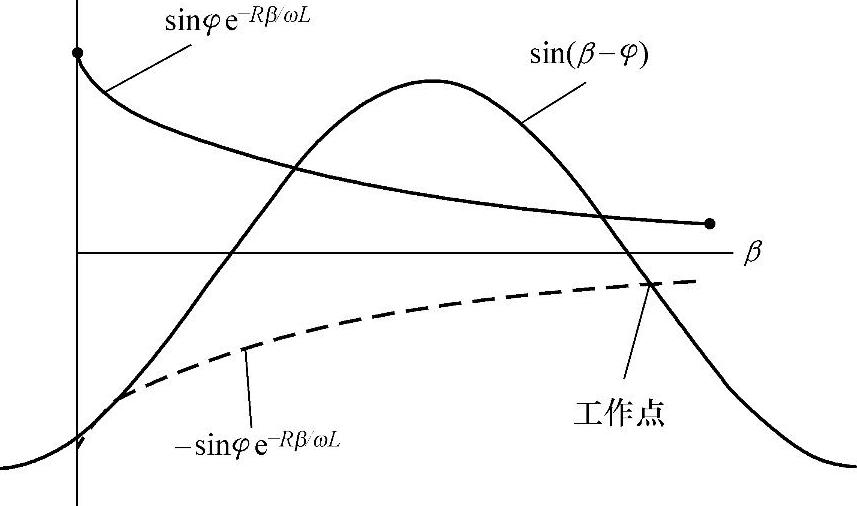
图5-3 熄弧角β的确定
在φ值较大时,相应的β值有(https://www.xing528.com)
β>π+φ
在纯电感负荷时达到终值2π(360°)。
建议:如果L>0,β>π+φ,由图5-4可看出,无法得出准确结果(历史问题β=π+φ)。
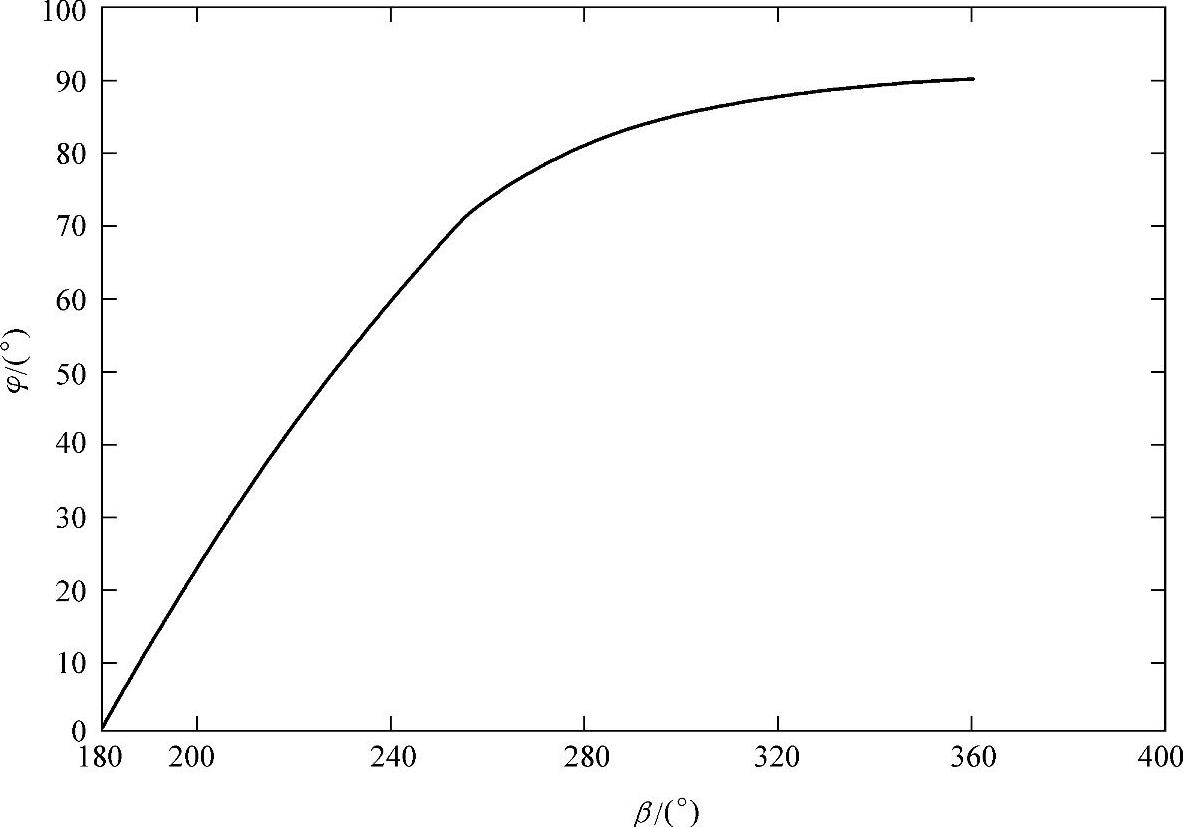
图5-4 β与φ的关系图
(2)迭代法1
在工作点为β≥π+φ时,
令β=π+φ
L1:计算x=sin(β-φ)
计算y=-e-Rβ/ωLsinφ
如果x=y,则β值即是正解,计算终止。
如果|x|<y,则增加β值,返回L1。
如果|x|>y,则减少β值,返回L1。
例5.1:一个单相半波二极管整流器,电源电压240V,频率50Hz,负荷R=10Ω,L=0.1H,用迭代法1求解β值。
解:由式(5-20)可知,φ=arctan(ωL/R)=72.34°
令β1=π+φ=252.34°。
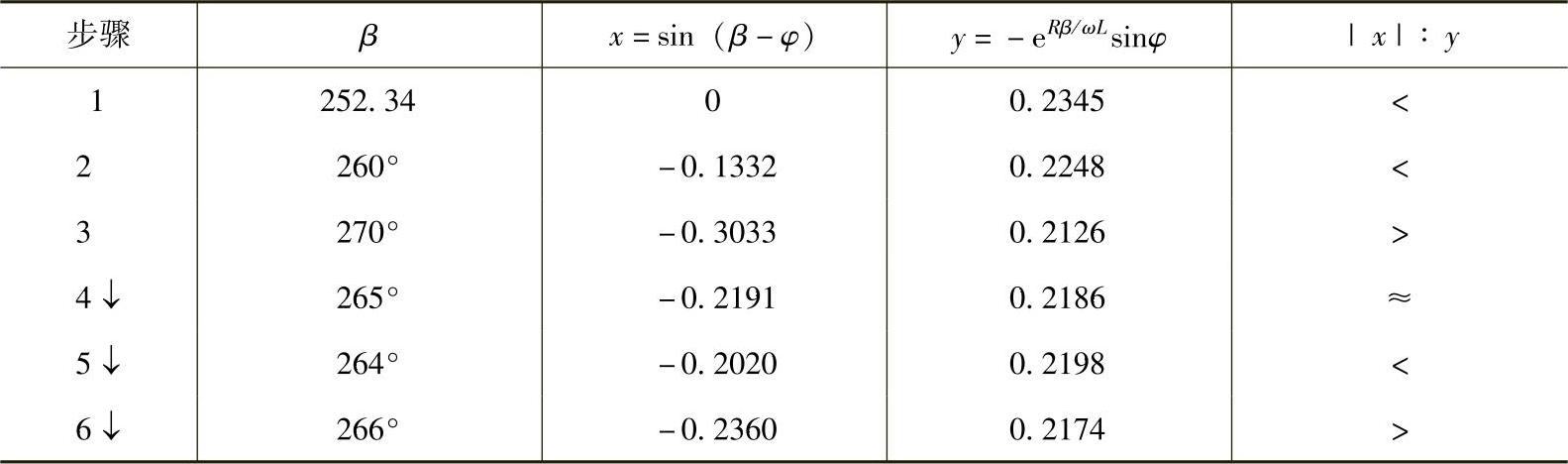
满足式(5-20)的最佳值是β=265°。
(3)迭代法2
令βn=π+φ
计算x=sin(β-φ)
L1:计算y=e-Rβ/ωLsinφ
令x=y
β(n+1)=[arcsiny]+π+φ
如果β(n+1)=βn,则计算终止。
否则,令βn=β(n+1),返回L1。
进行上述运算得到的高准确度熄弧角为β=264.972°。
整流后电流的平均值可通过下列计算得到:
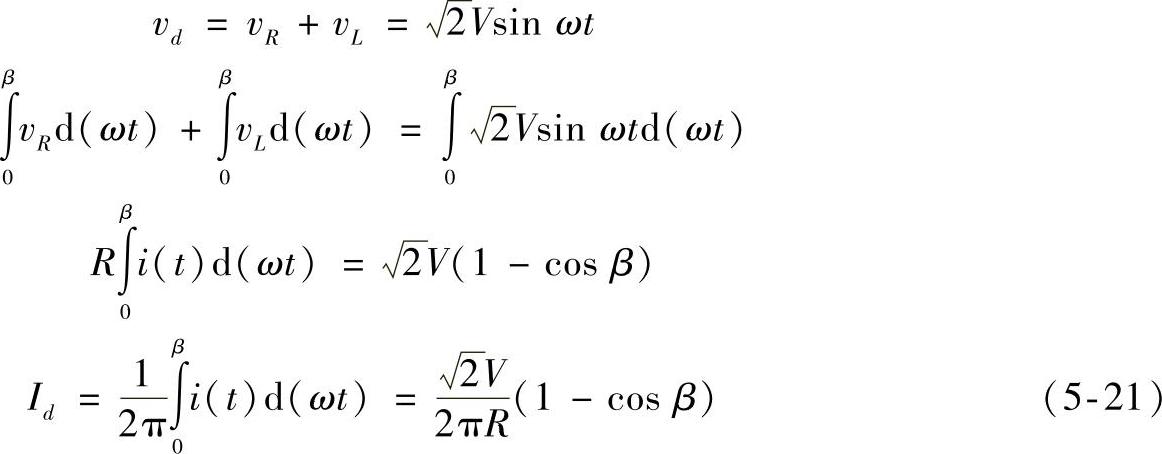
平均输出电压为

输出电压方均根值为
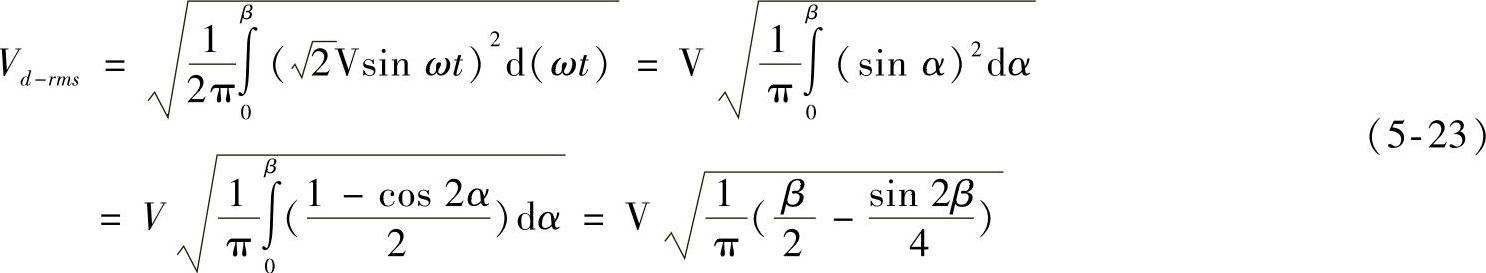
输出电压的波形系数和纹波系数分别为
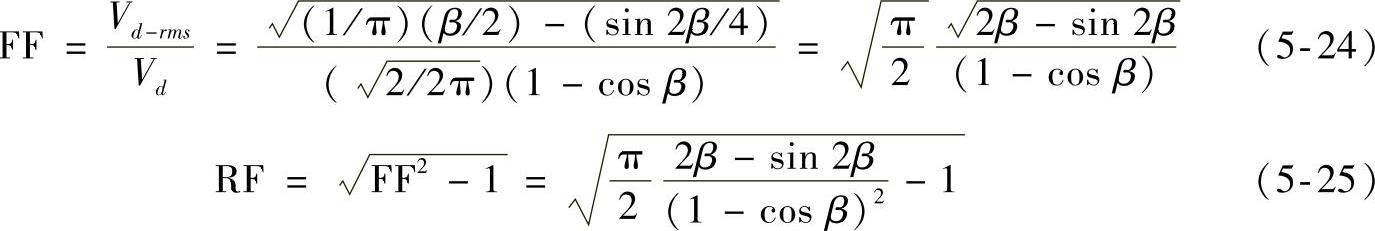
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




