快速傅里叶变换(Fast Fourier Transform,FFT)[9]是一种非常通用的波形分析方法。
角频率为ω的周期函数可用正弦函数级数表示:

式中,傅里叶系数为
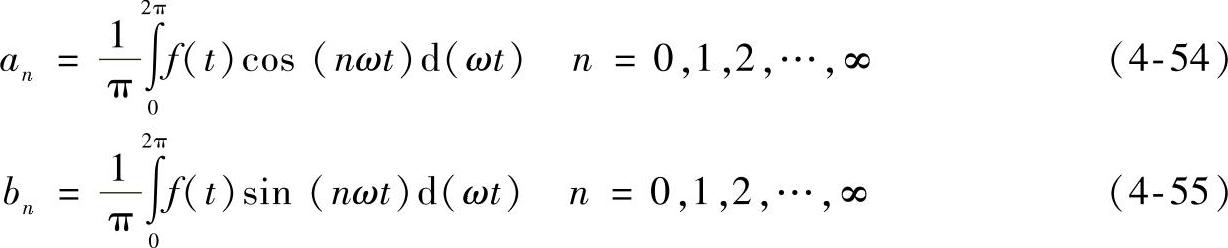
这种情况下,角频率为ω的部分叫做基波,角频率为nω(n>1)的部分叫做高次谐波。在频域中绘出所有谐波的幅值,可以得到各峰值的频谱。其中的a0/2是DC分量。
(1)中心对称周期函数
当一个周期函数为中心对称时,它的所有含余弦函数的部分消失,傅里叶变换公式变为

式中
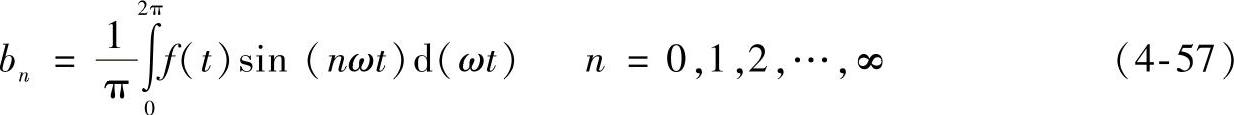
这类函数一般被称作奇函数。这种情况下,角频率ω的项为基波,角频率为nω(n>1)的各项为高次谐波。在频域中绘出各次谐波的幅值,可以得到各峰值的频谱。奇函数的DC分量为零。
(2)轴(镜像)对称周期函数
当周期函数为轴对称周期函数时,所有含正弦函数的项消失,傅里叶变换公式为
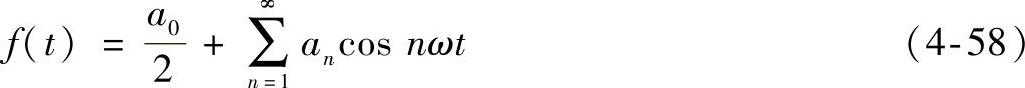
式中,a0/2是DC分量。
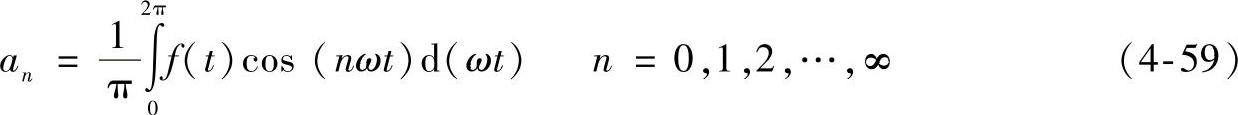
这类函数一般被称为偶函数。这种情况下,角频率为ω的项为基波,角频率为nω(n>1)的各项为高次谐波。在频域中绘出各次谐波的幅值,可以得到各峰值的频谱。在偶函数中,DC分量一般不为零。
(3)非周期函数
时域中周期函数的频谱在频域中是离散函数。如果函数是时域中的非周期函数,则可用傅里叶积分来表示,其频谱是频域中的连续函数。
(4)可用公式及数据
下面是一些可用于FFT的三角函数公式:

下面是某些常用特殊角度的相关函数值:
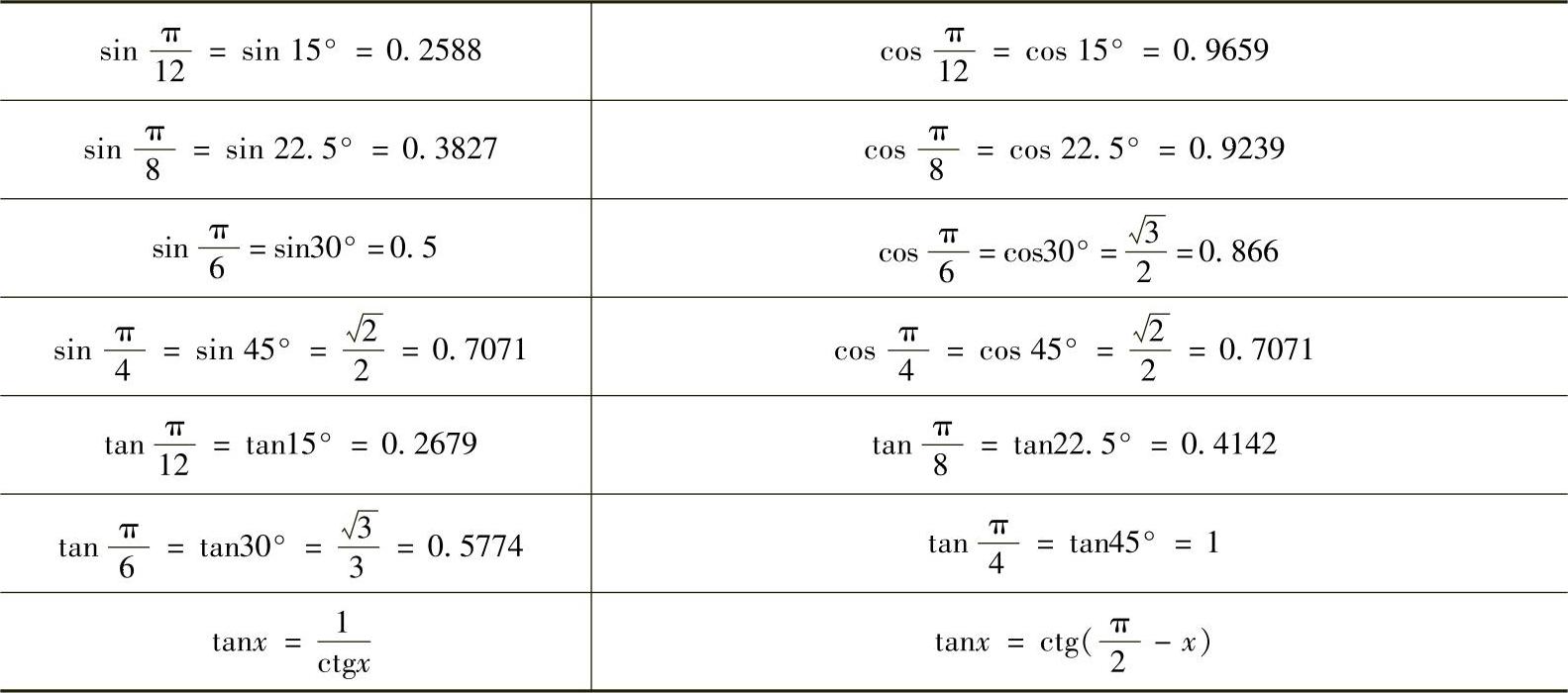
(5)FFT应用举例
例4.1:对于图4-8的奇方波函数曲线,计算FFT、7次及以下谐波的HF、THD和WTHD。
解:函数f(t)为
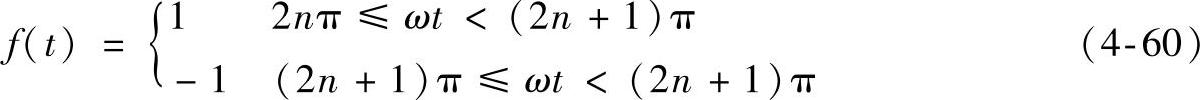
它的傅里叶系数为
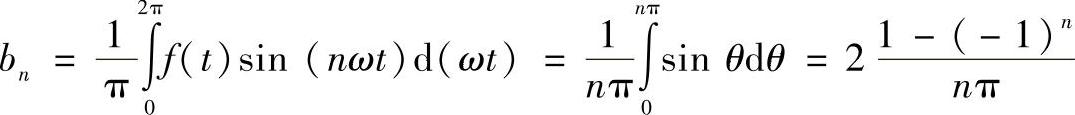
即
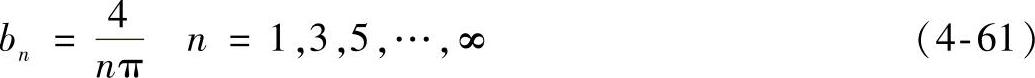
最终得到

它的基波幅值为4/π,考虑最高到7次的谐波,即n=3,5,7,则HF为
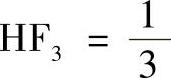 ;H
;H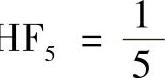 ;
;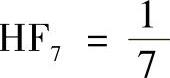
THD为
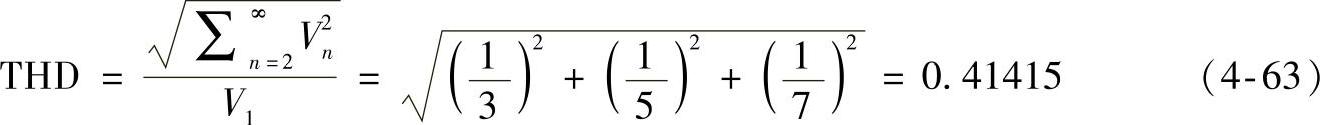
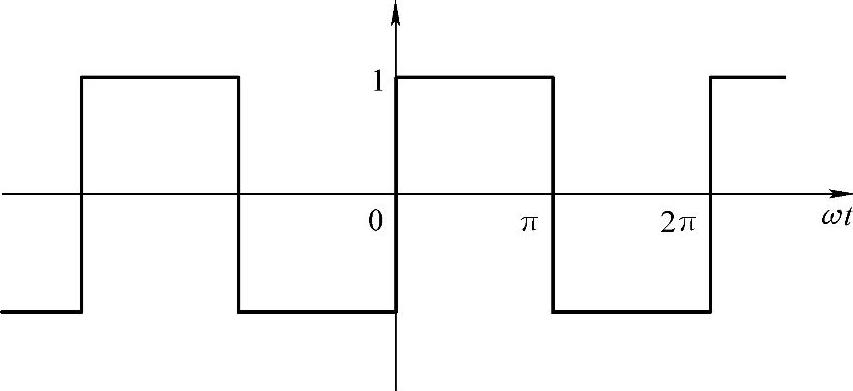
图4-8 例4.1的奇方波波形图

图4-9 例4.2的偶方波波形图
WTHD为
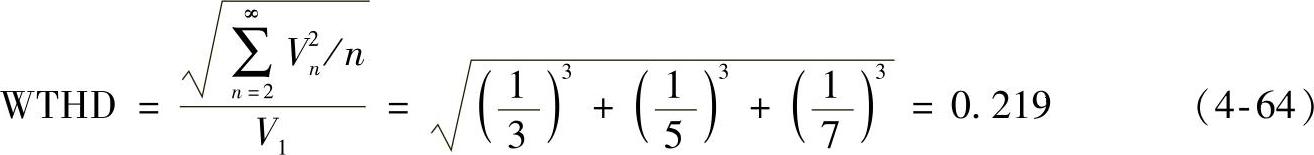
例4.2:偶方波函数曲线如图4-9所示,求出FFT、7次及以下谐波的HF、THD和WTHD。
解:函数f(t)为

它的傅里叶系数为
a0=0(https://www.xing528.com)
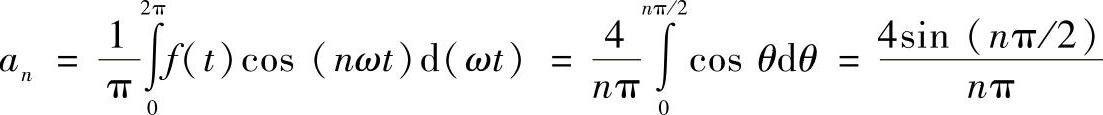
即
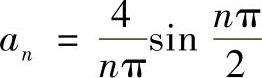 n=1,3,5,…,∞ (4-66)
n=1,3,5,…,∞ (4-66)
sinnπ/2的作用是确定正负号,最终得到
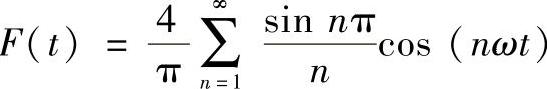 n=1,3,5,…,∞(4-67)
n=1,3,5,…,∞(4-67)
基波幅值为4/π,考虑最高到7次的谐波,即n=3,5,7,则HF为
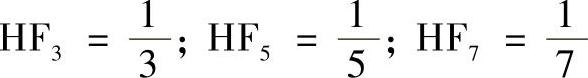
THD为

WTHD为
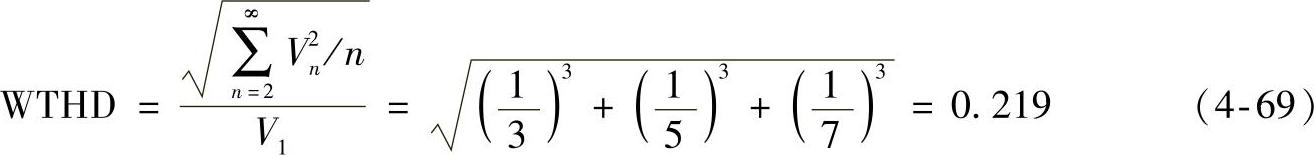
例4.3:图4-10是一个脉冲宽度为x的奇脉冲波函数曲线。求出FFT、最高到7次谐波的HF、THD和WTHD。
解:函数f(t)在周期-π到+π之间为

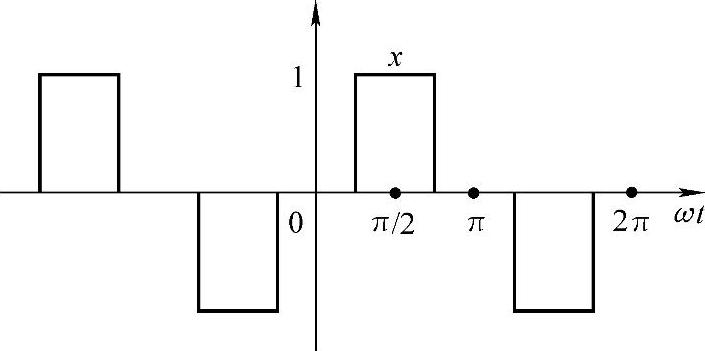
图4-10 例4.3的奇脉冲波形图
它的傅里叶系数为
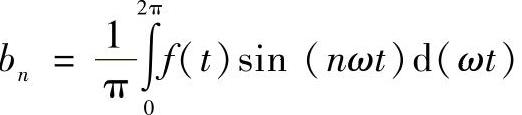
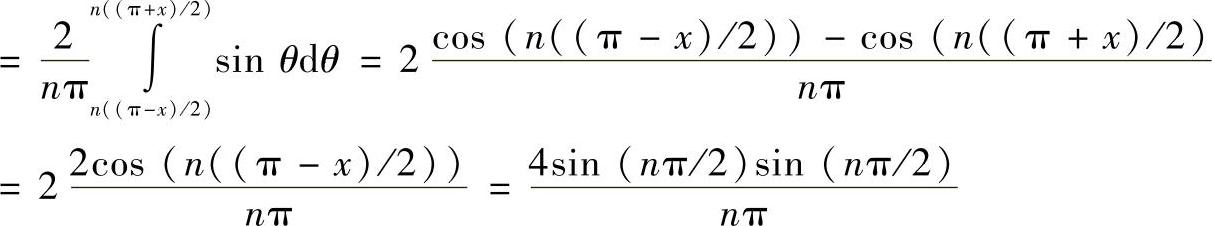
即
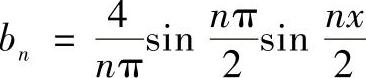 n=1,3,5,…,∞ (4-71)
n=1,3,5,…,∞ (4-71)
最终可得到
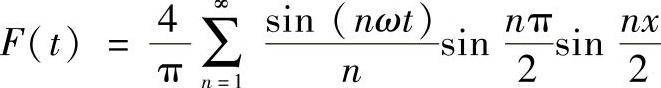 n=1,3,5,…,∞ (4-72)
n=1,3,5,…,∞ (4-72)
基波幅值为(4/π)sin(x/2)。考虑最高到7次谐波,即n=3,5,7,则HF为
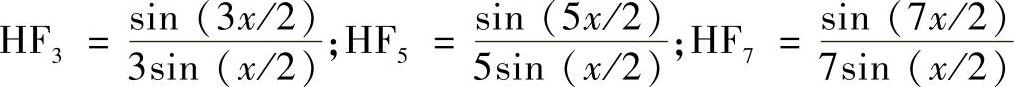
HF的数值均应为绝对值。
如果x=π,则THD为
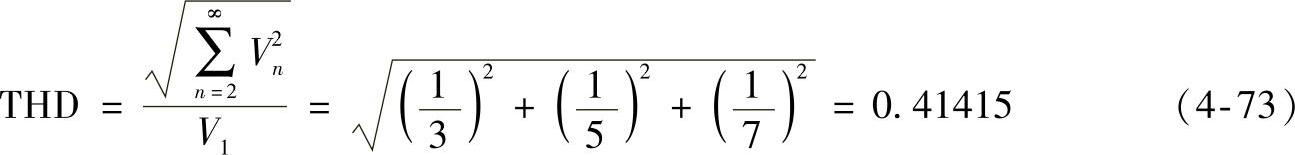
WTHD为

例4.4:图4-11是一个五级奇函数波。计算FFT、最高到7次谐波的HF、THD和WTHD。
解:函数f(t)在周期-π到+π之间为
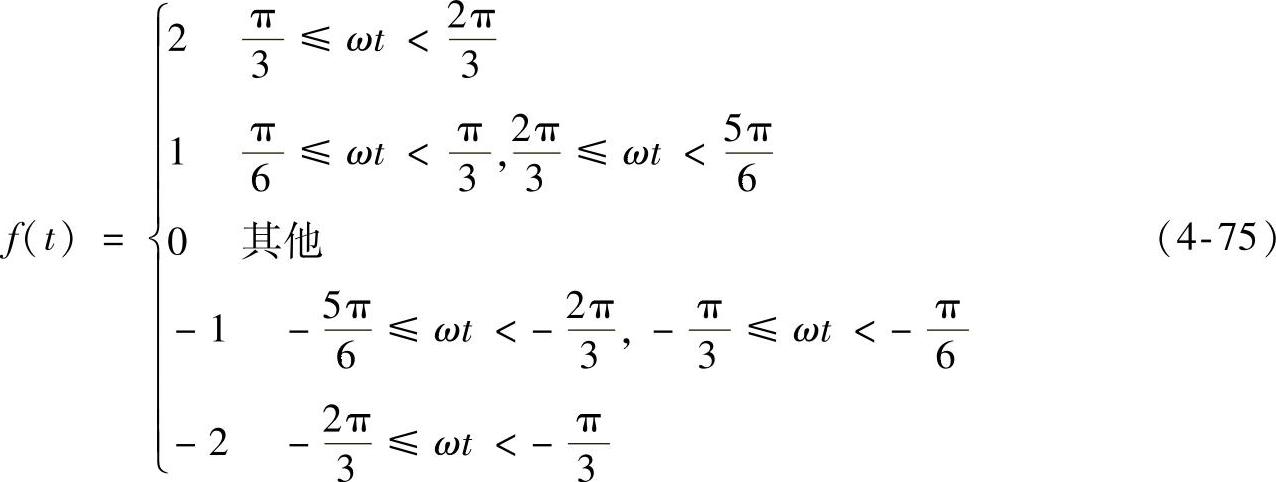

图4-11 例4.4的五级奇函数波形图
它的傅里叶系数为
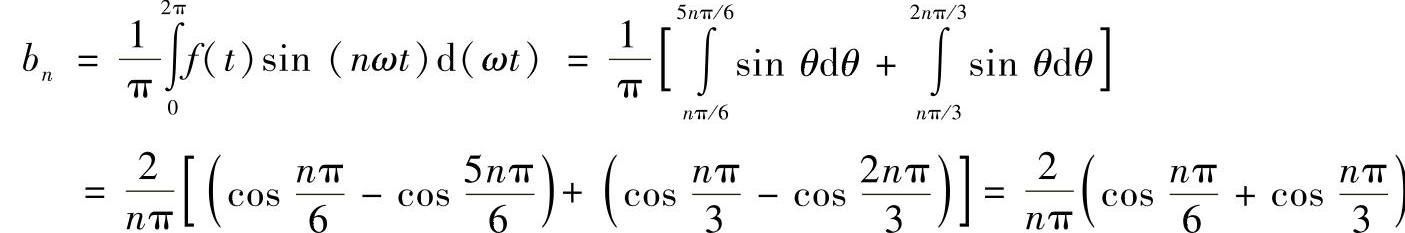
即
 n=1,3,5,…,∞(4-76)
n=1,3,5,…,∞(4-76)
最终可得到
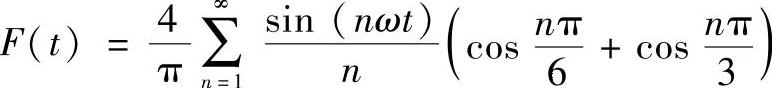 n=1,3,5,…,∞ (4-77)
n=1,3,5,…,∞ (4-77)
基波幅值为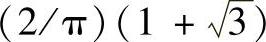 。考虑最高到7次谐波,即n=3,5,7,则HF为
。考虑最高到7次谐波,即n=3,5,7,则HF为
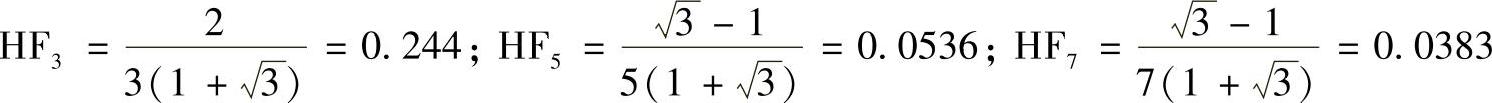
HF的数值均应为绝对值。
THD为
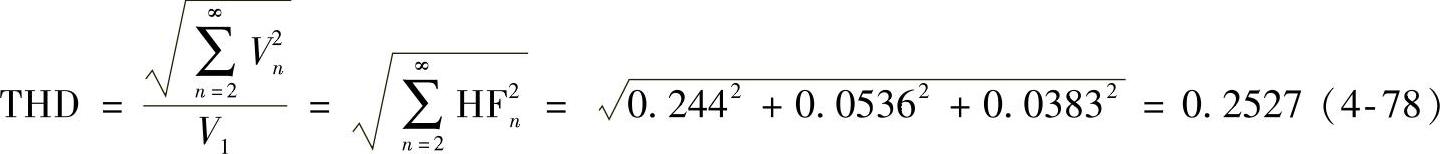
WTHD为
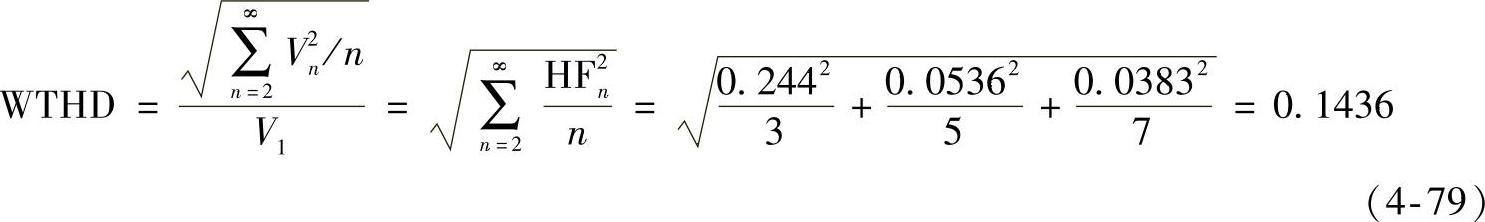
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




