其他因数和符号的作用与影响

传递函数是电路和系统中用来描述其动态特性的数学建模。施加输入信号，使用传递函数很容易获得系统的阶跃和脉冲响应。下列公式是一个典型的二阶传递函数^[6-8]：

式中，M为电压传输增益：M=V_o/V_in；τ为时间常数[见式（4-35）]；τ_d为阻尼时间常数[见式（4-37）]，τ_d=ξτ[见式（4-39）]；s为s域中的拉普拉斯算子。

使用这一数学模型，能够相当轻松地描述功率开关系统的特性。为了了解传递函数的更多特性，下面进行一些状态分析。

（1）极小阻尼时间常数

当阻尼时间常数非常小（即τ_d<<τ，ξ<<1）时，可将其忽略，忽略阻尼时间常数（即τ_d=0，ξ=0），则其传递函数降为一阶：

时域中单位阶跃函数响应为

g（t）=M（1-e^-t/τ） （4-42）

其暂态过程（稳定时间）接近时间常数的三倍，3τ，因此g（t）=g（3τ）=0.95M。图4-4中，τ_d=0的曲线是其时域中的响应。

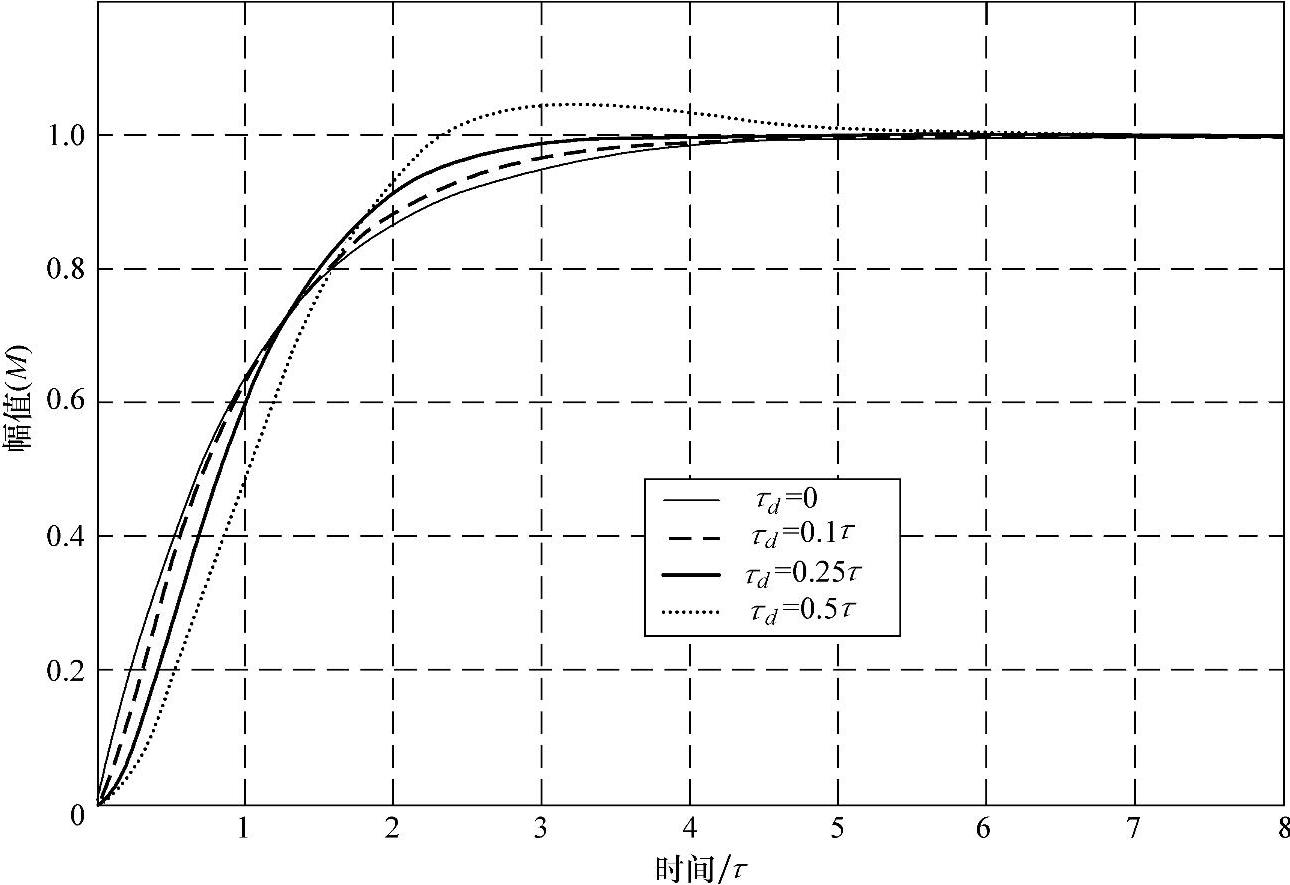
图4-4 单位阶跃函数响应（τ_d=0，0.1τ，0.25τ和0.5τ）

脉冲干扰响应为

Δg（t）=Ue^-t/τ （4-43）

式中，U为干扰信号。干扰恢复过程约为时间常数的三倍，3τ，因此g（t）=g（3τ）=0.95M。对应于图4-5中τ_d=0的曲线。

（2）小阻尼时间常数

当阻尼时间常数较小（即τ_d<τ/4，ξ<0.25）时，该常数不可忽略，τ_d值不能省略。式（4-40）提到的传递函数仍然为二阶函数，它有两个实极点-σ₁和-σ₂，公式如下：

式中

传递函数有两个实极点，假设σ₁>σ₂。时域中的单位阶跃响应为

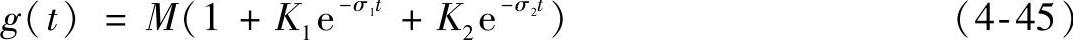
式中

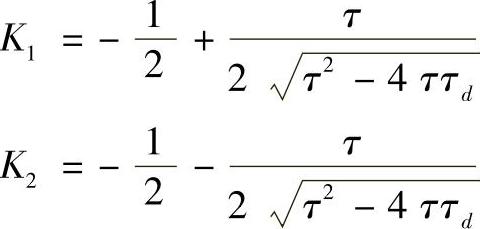
暂态过程约为时间值1/σ₁的三倍，3/σ₁<3τ。响应过程快速且无振荡。图4-4中τ_d=0.1τ的曲线为其在时域中的相应波形。

脉冲干扰响应为

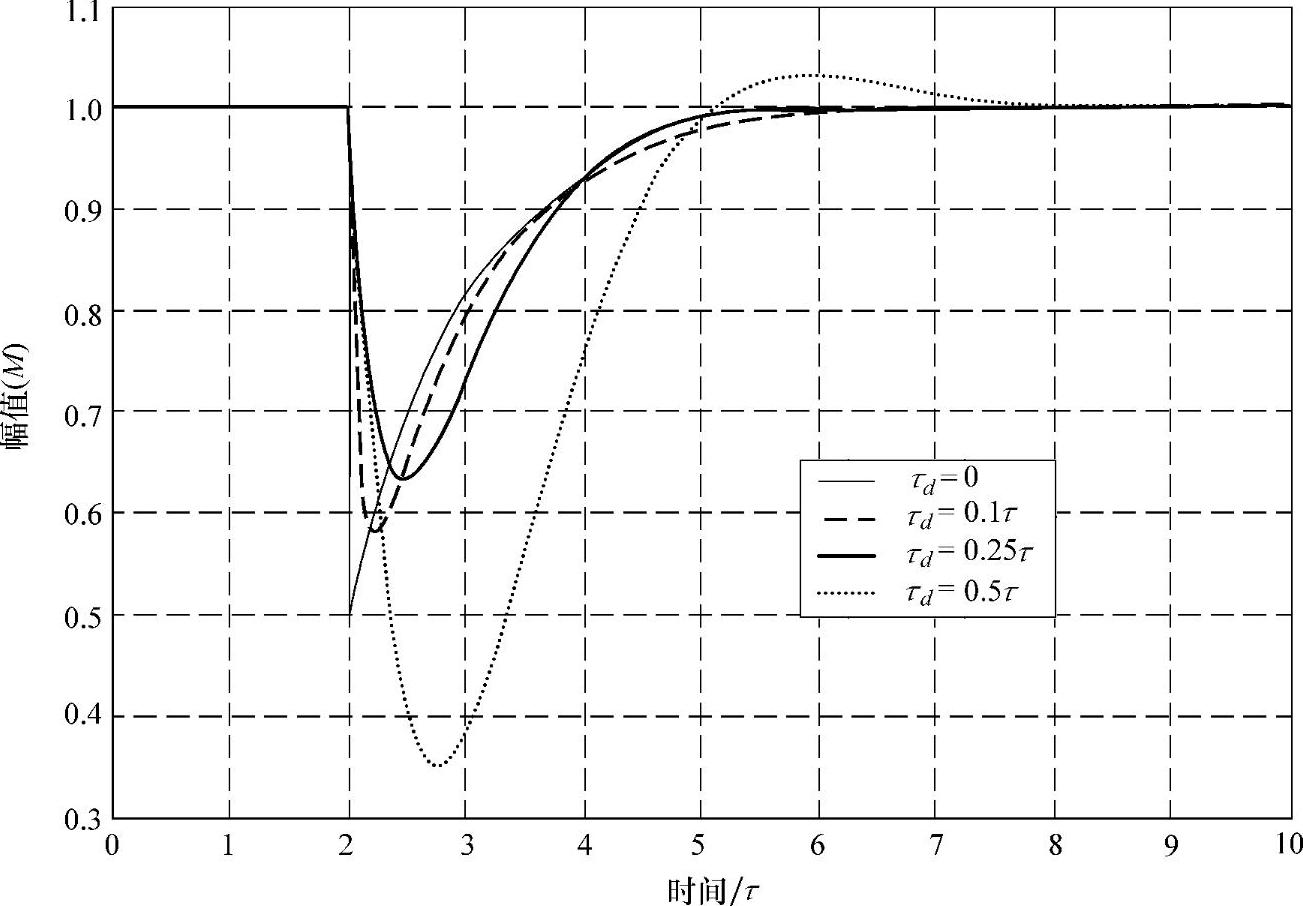
式中，U为干扰信号。暂态过程约为时间值1/σ₁的三倍，3/σ₁<3τ。图4-5中τ_d=0.1τ的曲线是该函数在时域中的响应波形。

(www.xing528.com)

图4-5 脉冲响应（τ_d=0，0.1τ，0.25τ和0.5τ）

（3）临界阻尼时间常数

当阻尼时间常数为临界值（即τ_d=τ/4）时，式（4-40）中的传递函数仍为二阶函数，有两个相等的实极点σ₁=σ₂=σ，公式如下：

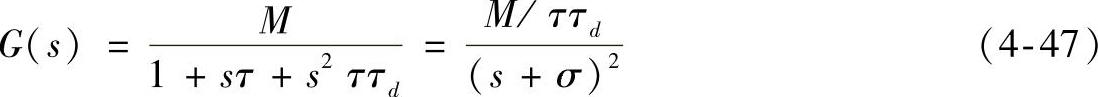
式中，σ=1/2τ_d=2/τ。

传递函数有双重实极点。该式说明了DC/DC变流器的特性。时域中的单位阶跃函数响应为

暂态过程接近时间常数的2.4倍，2.4τ。响应过程快速且无振荡。图4-4中τ_d=0.25τ的曲线为该函数在时域中的响应波形。

脉冲干扰响应为

式中，U为干扰信号。暂态过程仍约为时间常数的近2.4倍，即2.4τ。图4-5中τ_d=0.25τ的曲线是该函数在时域中的响应波形。

（4）大阻尼时间常数

当阻尼时间常数较大（即τ_d>τ/4，ξ>0.25）时，传递函数式（4-40）是一个含一对共轭复极点-s₁和-s₂的二阶函数，两个极点均在s域的左半平面（left-hand half plane，LHHP）内。

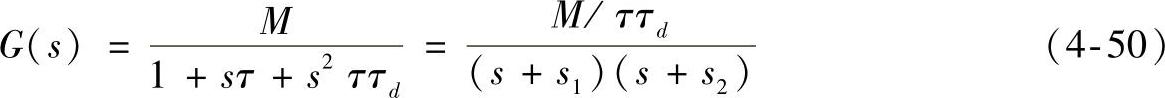
式中

s₁=σ+jω

s₂=σ-jω

该传递函数含一对共轭复极点-s₁和-s₂。该式也说明了DC/DC变流器的特性。它在时域中的单位阶跃函数响应为

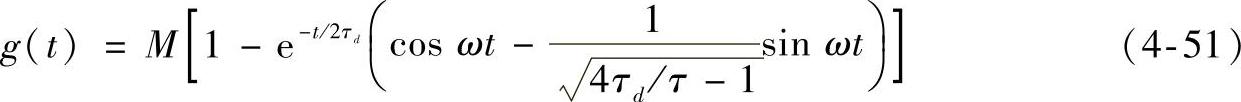
该暂态响应中含阻尼系数为σ、频率为ω的振荡过程。图4-4中τ_d=0.5τ的曲线和图4-6中τ，2τ，5τ和10τ的曲线为时域中的对应波形。

它的脉冲干扰响应为

式中，U为干扰信号。它的恢复过程是一条阻尼系数为σ、频率为ω的曲线。图4-5中τ_d=0.5τ的曲线和图4-7中τ，2τ，5τ和10τ的曲线为时域中的响应波形。

图4-6 单位阶跃函数响应（τ_d=τ，2τ，5τ和10τ）

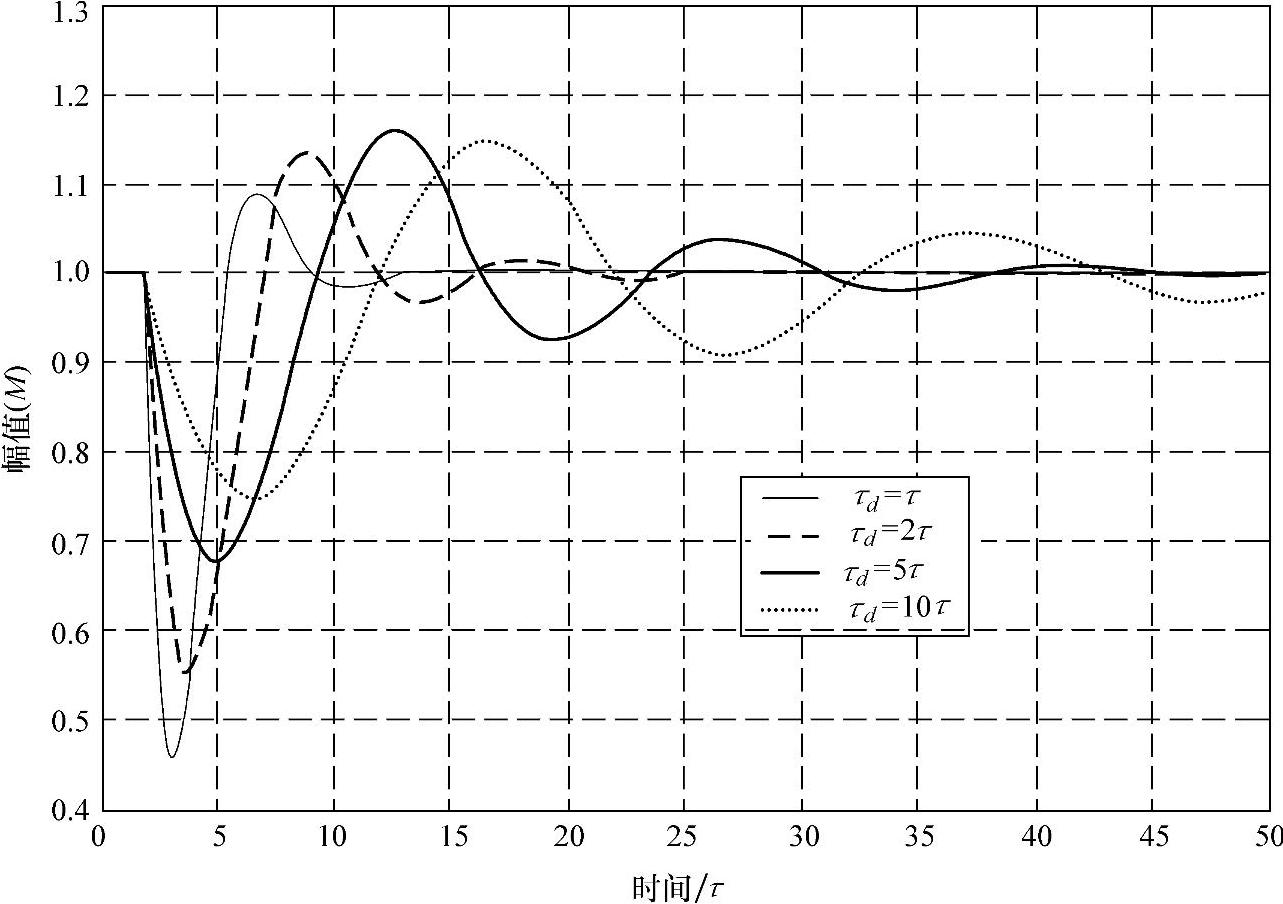
图4-7 脉冲响应（τ_d=τ，2τ，5τ和10τ）