熵编码算法简介

信息论给出无失真编码所需比特数的下限，为了逼近这个下限提出了一系列熵编码算法。熵编码是纯粹基于信号统计特性的编码技术，是一种无损编码，其基本原理是给出现概率较大的符号赋予一个短码字，而给出现概率较小的符号赋予一个长码字，从而使得最终的平均码长很小。常用的熵编码算法有赫夫曼(Huffman)编码，香农－范诺(Shannon－Fano)编码和算术编码，下面将对这些熵编码算法进行详细介绍。

7.2.2.1　赫夫曼(Huffman)编码

赫夫曼编码(Huffman Coding)，又称霍夫曼编码，是可变字长编码的一种。赫夫曼编码是Huffman于1952年提出的一种编码方法，该方法完全依据字符出现的概率来构造异字头的平均长度最短的码字，有时称之为最佳编码。简单来说，由于图像中表示颜色的数据出现的概率不同，赫夫曼编码对于出现频率高的赋予较短字长的码，对出现频率低的赋予较长字长的码，从而减少总的代码量，但不减少总的信息量。编码步骤如下:

(1)初始化，根据符号出现概率的大小，按照由大到小的顺序对符号进行排序；

(2)把概率最小的两个符号组成一个节点P1；

(3)重复步骤(2)，得到节点P2、P3和P4，形成一棵“树”，其中的P4称为根节点；

(4)从根节点P4开始到相应于每个符号的“树叶”，从上到下标上“0”(上枝)或者“1”(下枝)，至于哪个为“1”哪个为“0”则无关紧要，最后的结果仅仅是分配的代码不同，但代码的平均长度是相同的；

(5)从根节点P4开始顺着树枝到每个叶子分别写出每个符号的代码。

假如有A、B、C、D、E 5个字符，出现的频率(即权值)分别为5、4、3、2、1，那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1、2构成新树，其节点为1＋2＝3，虚线为新生成的节点，如图7－7所示。

第二步再把新生成的权值为3的节点放到剩下的集合中，所以集合变成{5，4，3，3}，再进行步骤(2)，取最小的两个权值构成新树，如图7－8所示；再依次建立赫夫曼树，如图7－9所示；其中将叶子节点的各个权值替换对应的字符，即为图7－10。

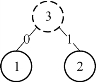
图7－7　取最小权值构造新树

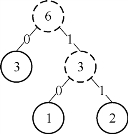
图7－8　取剩余集合中最小的两个权值构成新树

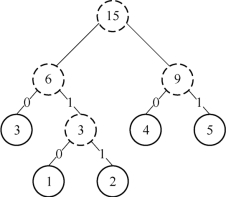
图7－9　建立赫夫曼树

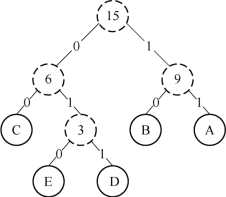
图7－10　将赫夫曼树中的叶子节点用字符代替

所以，各字符对应的编码为，A→11，B→10，C→00，D→011，E→010。赫夫曼编码的带权路径权值＝叶子节点的值×叶子节点的高度(根节点为0)，因此图7－10的带权路径长度为(3＋4＋5)×2＋(1＋2)×3＝33，至此，完成赫夫曼编码全过程。

7.2.2.2　香农－范诺(Shannon－Fano)编码

和赫夫曼编码一样，香农－范诺编码也是用一棵二叉树对字符进行编码，但在实际操作中，因为香农－范诺编码与赫夫曼编码相比编码效率较低，或者说编码平均码字较大，所以香农－范诺编码没有很大用处。但香农－范诺编码的基本思路还是可以参考的，实际的算法也很简单，具体的编码步骤如下:

(1)对于一个给定的符号列表，按符号出现的概率从大到小排序；

(2)将符号列表分为两部分，使左边部分符号出现的总频率和尽可能接近右边部分符号出现的总频率和；

(3)为该列表的左半边分配二进制数字0，右半边分配二进制数字1，这意味着，处于左半部分列表中的符号都将从0开始编码，右半部分列表中的符号都将从1开始编码；

(4)对列表的左边、右边递归进行步骤(3)和步骤(4)的操作，细分群体，并添加位的代码，直到每个符号都成为一个相应的代码树的叶即可结束。

举例展示香农－范诺编码的编码过程:表7－2展示了一组字母的出现次数及出现概率，并已经按照由大到小的顺序排列。

表7－2　各字母的出现次数及出现概率表

在字母B与C之间划定分割线，得到了左右两组字母，左右两组字母的总出现次数分别为22、17，这样的划分方式已经把两组的差别降到最小。通过这样的分割，A与B同时拥有了一个以0开头的编码，C、D、E则是以1开头的编码。随后，在树的左半边，于A、B间建立新的分割线，这样A就成了编码为00的叶子节点，B的编码为01，经过4次分割，得到一个树形编码。如表7－3所示，在最终得到的树中，拥有较大频率的符号为两位编码，其他两个频率较低的符号为三位编码。

表7－3　各字母最终编码表

根据A、B、C两位编码长度，D、E的三位编码长度，最终的平均码字长度为

7.2.2.3　算术编码

算术编码是一种无损数据压缩方法，也是一种熵编码的方法，和其他熵编码方法不同的地方在于，其他的熵编码方法通常是把输入的消息分割为符号，然后对每个符号进行编码，而算术编码将整个要编码的数据映射到一个位于[0，1)的实数区间中，利用这种方法算术编码可以让压缩率无限地接近数据的熵值，从而获得理论上的最高压缩率。算术编码用到两个基本的参数:信源符号的概率和它的编码间隔。信源符号的概率决定压缩编码的效率，也决定编码过程中符号的间隔，而这些间隔包含在0～1之间。编码过程中的间隔决定了符号压缩后的输出值区间。

算术编码可以是静态的或者自适应的。在静态算术编码中，信源符号的概率是固定的，而在自适应算术编码中，信源符号的概率根据编码时符号出现的频繁程度动态地进行修改。需要开发动态算术编码是因为事先知道精确的概率是很难的，而且是不切实际的，当压缩消息时，我们不能期待一个算术编码器获得最大的效率，所能做的最有效的方法是在编码过程中估算概率，因此动态建模就成为确定编码器压缩效率的关键。在自适应算术编码中，在编码开始时，各个符号出现的概率相同，都为1/n，随着编码的进行再更新出现概率。

算术编码步骤如下。

(1)编码器在开始时将“当前间隔”[L，H)设置为[0，1)。

(2)对每一个输入事件，编码器按下面的步骤进行处理:(www.xing528.com)

①编码器将“当前间隔”分为若干个子间隔，每一个事件一个子间隔，一个子间隔的大小与将出现的事件的概率成正比；

②编码器选择与下一个发生事件相对应的子间隔，并使它成为新的“当前间隔”。

(3)最后输出的“当前间隔”的下边界就是该给定事件序列的算术编码。

在算术编码中需要注意以下几个问题。

(1)由于实际计算机的精度不可能无限长，运算中出现溢出是一个不可避免的问题，但多数机器都有16位、32位或者64位的精度，因此这个问题可以使用比例缩放方法解决。

(2)算术编码器对整个消息只产生一个码字，这个码字是在间隔[0，1)中的一个实数，因此译码器在接收到表示这个实数的所有位之前不能进行译码。

(3)算术编码是一种对错误很敏感的编码方法，如果有一位发生错误就会导致整个消息译错。

下面列举两个例子分别展示静态算术编码和自适应算术编码的编码过程。

【例7－4】　在静态算术编码中，假设信源符号为{A，B，C，D}，这些符号的概率分别为{0.1，0.4，0.2，0.3}，根据这些概率可把间隔[0，1)分成4个子间隔:　[0，0.1)，[0.1，0.5)，[0.5，0.7)，[0.7，1)，其中[x，y)表示半开放间隔，即包含x不包含y。将题目信息整合为表7－4。

表7－4　信源符号、概率和初始编码间隔

如果二进制消息序列的输入为CADACDB。编码时首先输入的符号是C，找到它的编码范围是[0.5，0.7)；由于消息中第2个符号A的编码范围是[0，0.1)，因此它的间隔就取[0.5，0.7)的第1个1/10作为新间隔[0.5，0.52)；依此类推，编码第3个符号D时取新间隔为[0.514，0.52)，编码第4个符号A时取新间隔为[0.514，0.514 6)，…。消息的编码输出可以是最后一个间隔中的任意数。整个编码过程如图7－11所示。

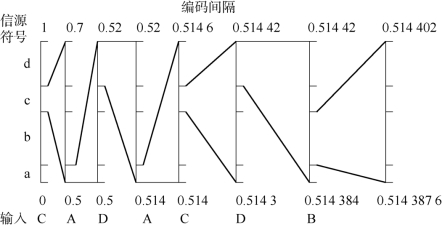
图7－11　静态算术编码的编码过程

取一个0.514 387 6～0.514 402之间的数0.514 387 6，将十进制小数转换为二进制，此时，(0.514 387 6)D≈(0.100 000 1)B，去掉小数点和前面的0，得1000001，所以CADACDB的编码为1000001，长度为7。编码和译码的全过程如表7－5和表7－6所示。

表7－5　编码过程

表7－6　译码过程

【例7－5】　在自适应算术编码中，假设一份数据由A、B、C 3个符号组成，现在要编码数据BCCB，编码过程如图7－12所示。

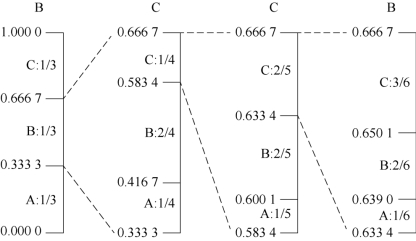
图7－12　自适应算术编码的编码过程

(1)算术编码从区间[0，1)开始，这时3个符号的概率都是1/3，按照这个概率分割区间。

(2)第1个输入的符号是B，所以我们选择子区间[0.333 3，0.666 7)作为下一个区间。

(3)输入B后更新概率，根据新的概率对区间[0.333 3，0.666 7)进行分割。

(4)第2个输入的符号是C，选择子区间[0.583 4，0.666 7)。

(5)以此类推，根据输入的符号继续更新频度、分割区间、选择子区间，直到符号全部编码完成。

最后得到的区间是[0.639 0，0.650 1)，输出属于这个区间的一个小数，如0.64。那么经过算术编码的压缩，数据BCCB最后输出的编码就是0.64。

算术编码进行解码时仅输入一个小数，整个过程相当于编码时的逆运算。解码过程如下。

(1)解码前首先需要对区间[0，1)按照初始时的符号频度进行分割，然后观察输入的小数位于哪个子区间，输出对应的符号。

(2)之后选择对应的子区间，然后从选择的子区间中继续进行下一轮的分割。

(3)不断地进行这个过程，直到所有的符号都解码出来。

在本例中，输入的小数是0.64。

(1)初始时3个符号的概率都是1/3，按照这个概率分割区间。

(2)根据上图可以发现0.64落在子区间[0.333 3，0.666 7)中，于是可以解码出B，并且选择子区间[0.333 3，0.666 7)作为下一个区间。

(3)输出B后更新频度，根据新的概率对区间[0.333 3，0.666 7)进行分割。

(4)这时0.64落在子区间[0.583 4，0.666 7)中，于是可以解码出C。

(5)按照上述过程进行，直到所有的符号都解码出来。

可见，只需要一个小数就可以完整还原出原来的所有数据。