几何校正方法解析：空间变换技术

几何校正一般是指通过一系列的数学模型来改正和消除遥感影像成像时因摄影材料变形、物镜畸变、大气折光、地球曲率、地球自转、地形起伏等因素导致的原始图像上各个物体的几何位置、形状、尺寸、方位等特征与在参照系统中的表达要求不一致时产生的变形。

几何校正分为两个步骤:一是空间变换，即对图像平面上的像素进行重新排列以恢复原空间关系；二是灰度插值，即对空间变换后的像素赋予相应的灰度值以恢复原位置的灰度值。

图6－14　典型的非系统失真

(a)地球自转；(b)高度变化；(c)俯仰；(d)速度变化；(e)流动；(f)偏航

6.4.2.1　空间变换

空间变换是对图像平面上的像素进行重新排列以恢复原空间关系，即将输入图像的像素位置映射到输出图像的新位置。

几何形变可以表示为

式中:(x′，y′)——校正图的空间坐标点；

s(x，y)和t(x，y)——产生几何失真图像的2个空间变换。

对线性失真，s(x，y)和t(x，y)可写为

对一般的非线性二次失真，s(x，y)和t(x，y)可写为

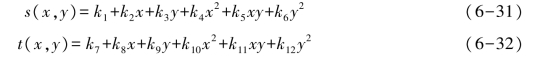
如果已知s(x，y)和t(x，y)的表达式，就可以通过反变换来恢复图像。但实际中通常不知道表达式，可用约束对应点法(或称连接点)解决，如图6－15所示。

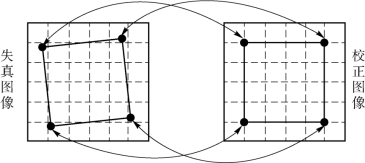
图6－15　失真图和校正图的连接点

如图6－15所示，利用“连接点”建立失真图像和校正图像间像素空间位置的对应关系，而这些“连接点”在输入(失真)图像和输出(校正)图像中的位置是精确已知的。两个四边形区域的顶点可作为对应点，设在四边形区域内的几何失真过程可用一对双线性等式表示，即

可得到

由图6－15可知，两个四边形区域共有4组(8个)已知对应点，所以8个系数ki可以全部解得，根据这些系数可建立将四边形区域内的所有点进行空间映射的公式。一般来说，可将1幅图分成一系列覆盖全图的四边形区域的集合，对每个区域都找足够的对应点以计算进行映射所需的系数，即可完成空间变换过程。

6.4.2.2　灰度插值

图像经几何位置校正后，在校正空间中各像素点的灰度值等于被校正图像对应点的灰度值，但是一般校正后的图像某些像素点可能分布不均匀，不会恰好落在坐标点上，因此常采用内插法来求得这些像素点的灰度值。经常使用的方法有最近邻插值(Nearest neighbor interpolation)、双线性插值(Bi－linear interpolation)和三次样条插值(Cubic spline interpolation)。

最近邻插值通常被用于图像缩放中，即在原图中选取一个与映射点最靠近的像素作为缩放图某点的像素值，如图6－16所示。最近邻插值首先将缩放图坐标(x，y)经空间变换映射为原图像中的(x′，y′)，如果(x′，y′)是非整数坐标，则寻找(x′，y′)的最近邻，并将最近邻的灰度值赋给缩放图像(x，y)处的像素。这种方法实现起来非常方便，但不够精确，甚至经常产生不希望的人为疵点，如高分辨率图像直边的扭曲等。因此，可以采用更完善的技术得到较平滑的结果，如样条插值、立方卷积内差等，但是更平滑的近似会增加计算的开销。

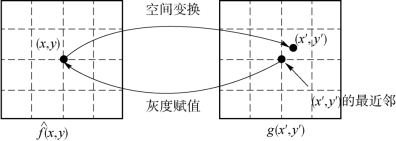
图6－16　最近邻灰度插值示意

双线性插值示意如图6－17所示，利用点(x′，y′)的4个最近邻的灰度值来确定(x′，y′)处的灰度值。设(x′，y′)的4个最近邻为A、B、C、D，它们的坐标分别为(i，j)、(i＋1，j)、(i，j＋1)、(i＋1，j＋1)，其灰度分别为g(A)、g(B)、g(C)、g(D)。

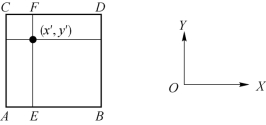
图6－17　双线性插值示意

首先计算E和F这两点的灰度值g(E)，g(F)为

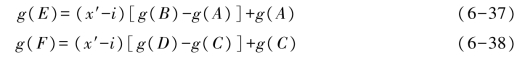
则(x′，y′)点的灰度值g(x′，y′)为(www.xing528.com)

图6－18展示了不同灰度插值的结果比较，由图可知，双线性插值的效果好于最近邻插值变换的效果。

图6－18　不同灰度插值的结果比较

(a)原始图像；(b)最近邻插值；(c)双线性插值

三次样条插值函数是分段三次多项式，在每个小区间[xi，xi＋1]上可以写成

式(6－40)中共有4n个待定参数。S(x)在[a，b]上二阶导数连续，故在内节点xi(i＝1，2，…，n－1)处应满足连续性条件

其中，S(k)(xi－0)是点xi的k阶左导数，S(k)(xi＋0)是点xi的k阶右导数，那么由上式可产生3(n－1)个条件，再加上n＋1个插值条件，共有4n－2个条件，因此，还需要2个条件就能确定S(x)。通常在区间端点a＝x0和b＝xn上各加一个条件，我们将这个条件称为边界条件，即可确定S(x)。常用的边界条件确定方式有以下3种。

(1)已知两端的二阶导数值，即

其特殊情况为

对应的样条函数称为自然样条。

(2)已知两端的一阶导数值，即

(3)周期边界条件

此时，对函数值有周期条件f(x0)＝f(xn)。

三次样条插值较难以理解，下面举例说明。样条插值法可以简单理解为每两个点之间确定一个函数，这个函数就是一个样条，函数不同，样条就不同，然后把所有样条分段结合成一个函数，就是最终的插值函数。线性样条就是用两点确定一条直线，我们可以在每两点间画一条直线，就可以把所有点连起来。线性样条如图6－19所示，显然曲线不够光滑，究其原因是连接点处导数不相同。

因为直线对点的拟合效果不好，所以就用曲线代替，而二次函数是最简单的曲线。如图6－20所示，假设4个点x0、x1、x2、x3，有3个区间，需要3个二次样条，每个二次样条为ax2＋bx＋c，故总计9个未知数。

图6－19　线性样条

图6－20　点的位置示意

x0、x3两个端点都有一个二次函数经过，可确定2个方程；x1、x2两个中间点都有两个二次函数经过，可确定4个方程；中间点处必须连续，需要保证左右二次函数一阶导相等，即2a1x1＋b1＝2a2x1＋b2，2a2x2＋b1＝2a3x1＋b3，可确定2个方程，此时有了8个方程。此外，假设第一个方程的二阶导为0，即a1＝0，又是一个方程，共计9个方程，联立即可求解。二次样条插值连续光滑。因为假设a1＝0，所以二次函数变成b1x＋c1，使得前两个点之间是条直线，最后两个点之间有些过于陡峭。二次样条函数如图6－21所示，三次样条函数如图6－22所示。

二次函数最高项系数为0，其变成直线；三次函数最高项系数为0，还是曲线，插值效果应该更好。三次样条思路与二次样条基本相同，同样假设4个点x0、x1、x2、x3，有3个区间，需要3个三次样条，每个三次样条为ax3＋bx2＋cx＋d，故总计12个未知数。

内部节点处的函数值应该相等，这里一共是4个方程；函数的第一个端点和最后一个端点，应该分别在第一个方程和最后一个方程中，这里是2个方程；两个函数在节点处的一阶导数应该相等，这里是2个方程；两个函数在节点处的二阶导数应该相等，这里是2个方程；假设端点处的二阶导数为0，这里是2个方程；共计12个方程，联立即可求解。由图6－21和图6－22可得，三次样条函数相较于二次函数而言，取得了更好的拟合效果。

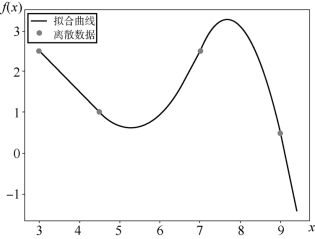
图6－21　二次样条函数

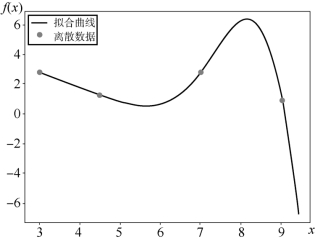
图6－22　三次样条函数