约束最小二乘方滤波优于维纳滤波处理高、中噪声图像

在数学应用上，对于运动引起的图像模糊，最简单的方法是直接做逆滤波，但是逆滤波对加性噪声特别敏感，使得恢复的图像几乎不可用。维纳滤波器是一种自适应最小均方差滤波器，维纳滤波的方法是一种统计方法，用来去除含有噪声的模糊图像，其目标是找到未污染图像的一个估计，使它们之间的均方差最小，可以去除噪声，同时清晰化模糊图像。

式中: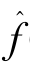(x，y)——维纳滤波后的图像；

f(x，y)——清晰的原始图像。

由安德鲁斯(Andrews)和亨特(Hunt)推导满足这一要求的传递函数为

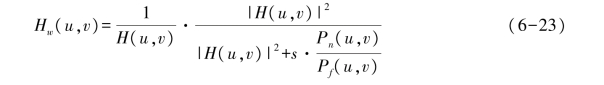
则有

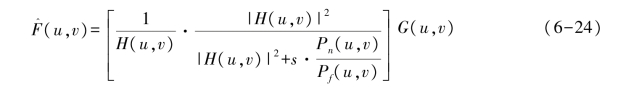
式中: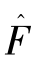(u，v)——复原图像的傅里叶变换；

G(u，v)——退化图像的傅里叶变换；

H(u，v)——退化函数；

Pn(u，v)——噪声的功率谱，Pn(u，v)＝｜N(u，v)｜2；

Pf(u，v)——原始图像的功率谱，Pf(u，v)＝｜F(u，v)｜2；

s＝，λ为常数，是拉格朗日乘数。

维纳滤波需要知道原始图像和噪声的二阶统计特性，即要知道关于图像和噪声的先验知识，如Pf(u，v)，Pn(u，v)，但是这恰恰也是我们不知道的，这也是维纳滤波器的局限所在，因此我们一般将上述两个公式的比值看作是常数K代入进行计算，即K与噪声和未退化图像之间的信噪比有关，K在不同情况下取值不同。那么，维纳滤波的计算公式为

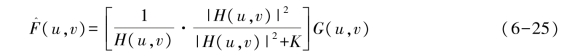
这是一种无可奈何的粗糙的近似，但是当噪声为白噪声即其功率谱为常数的时候，这种近似效果很不错。维纳滤波处理前后的图像如图6－11所示。

图6－11　维纳滤波处理前后的图像

(a)原图；(b)运动模糊后的图像；(c)维纳滤波；(d)运动模糊、高斯噪声后的图像；(e)NSR＝0维纳滤波；(f)基于估计NSR的维纳滤波

从图6－11(a)(b)　(c)可以看出，若无噪声，此时维纳滤波相当于逆滤波，恢复运动模糊效果是极好的；从图6－11(d)(e)(f)可以看出，信噪比^[3]估计的准确性对图像影响是比较大的，图6－11(e)效果几乎不可用。(www.xing528.com)

6.3.3　约束最小二乘方滤波

约束最小二乘方滤波是图像复原中一种较好的方法。由于逆滤波对噪声特别敏感，因此约束最小二乘方滤波的核心是针对噪声的敏感性问题，以平滑度量的最佳复原为基础，减少噪声敏感，消除很严重的噪声，进而复原图像；维纳滤波要求未退化图像和噪声的功率谱必须是已知的，但是通常这两个功率谱很难估计，尽管可以用一个常数去估计功率谱比，然而并不总是一个合适的解，而约束最小二乘方滤波只要求知道噪声的方差和均值，并且这些参数可通过给定的退化图像计算出来，这是约束最小二乘方滤波的一个重要优点。

由于约束最小二乘方滤波代数实现方法相当复杂，因此这里直接给出约束最小二乘方滤波的表达式，即

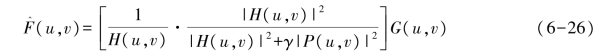
式中:γ——参数；

P(u，v)——矩阵p(x，y)＝[0，－1，0；－1，4，－1；0，－1，0]的傅里叶变换。该算法相比于维纳滤波，对其应用的每幅图像都能产生最优的结果。在MATLAB实现过程中，约束最小二乘方滤波通过函数deconvreg来实现，其语法为

fr＝deconvreg(g，PSF，NOISEPOWER，RANGE)

其中:g——被污染的图像；

fr——复原的图像；

PSF——点扩展函数；

RANGE——值的范围；

NOISEPOWER与｜｜η｜｜2成比例。

图6－12是对图像在不同情况下进行约束最小二乘方滤波处理的对比图。

经过对比可得，约束最小二乘方滤波对高噪声和中等噪声产生结果要好于维纳滤波，对于低噪声而言，两种滤波产生结果基本相同。

图6－12　约束最小二乘方滤波后的对比图

(a)原图；(b)运动模糊后的图像；(c)逆滤波

图6－12　约束最小二乘方滤波后的对比图(续)

(d)运动模糊、高斯噪声后的图像；(e)约束最小二乘方滤波；(f)去模糊deconvreg函数