图像退化在频域的关系表达式为G(u，v)＝F(u，v)H(u，v)＋N(u，v)，若图像退化过程中没有噪声的影响，那么图像退化的频域关系表达式变为G(u，v)＝F(u，v)H(u，v)，那么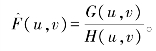
其中，G(u，v)为退化图像的傅里叶变换，F(u，v)为原始图像的傅里叶变换，
为复原图像的傅里叶变换，H(u，v)为退化系统的频率响应，N(u，v)为噪声信号的傅里叶变换，H－1(u，v)称为逆滤波器。这就表明若噪声为0，则采用逆滤波恢复法能完全再现原图像，但实际上碰到的问题都是有噪声的，因而只能在有噪声的情况下产生复原图像
即
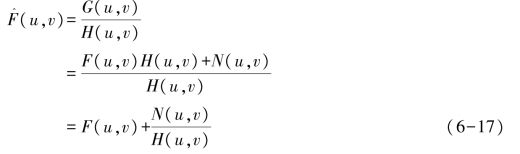
若噪声存在，并且H(u，v)很小或为0，则噪声被放大，这意味着退化图像中小噪声的干扰在H(u，v)较小时，会对逆滤波恢复的图像产生很大的影响，有可能使恢复的图像
和原图像f(x，y)相差很大，甚至面目全非。为此，改进的方法有如下3种。
(1)在H(u，v)＝0处不做计算，即逆滤波为
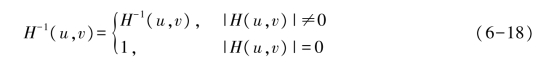
(2)当H(u，v)非常小时，N(u，v)/H(u，v)对复原结果起着主导作用，而在大多数图像系统中，｜H(u，v)｜离开原点衰减很快，因此复原应局限于距离原点不远的有限区域内进行。逆滤波器为
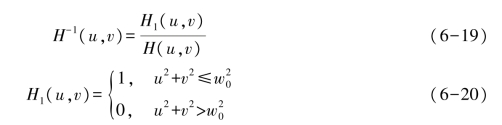
式中:H1(u，v)——理想低通滤波器。
这种方法的缺点是会出现振铃效应。(www.xing528.com)
(3)为避免振铃效应，有一种改进的方法，即
其中，k和d均为小于1的常数，且d应选得较小。
逆滤波处理前后的图像如图6－10所示。
从图6－10(e)可以看出，对含有噪声的模糊图像采用逆滤波恢复法的恢复效果极差，但从图6－10(f)可知，若知道图像中的噪声分布，也是可以完全复原图像信息的。因此可知，逆滤波在图像没有噪声的情况下是很好的，但是它对噪声非常敏感，除非我们知道噪声的分布情况，否则逆滤波几乎不可用，但事实上，图像中噪声的分布情况很难预知。
图6－10 图像复原对比图
(a)原图；(b)运动模糊后的图像；(c)逆滤波；(d)运动模糊、高斯噪声后的图像；(e)噪声未知直接逆滤波；(f)噪声已知逆滤波
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
