噪声在图像上常表现为引起较强视觉效果的孤立像素点或像素块，一般噪声信号与要研究的对象不相关，它以无用的信息形式出现，扰乱图像的可观测信息，通俗地说就是噪声让图像不清楚。
数字图像的噪声主要来源于两个方面，一是来源于图像的获取过程中，会受到图像传感器的质量和环境的影响。两种常用类型的图像传感器分别是CCD和CMOS，在采集图像的过程中，由于受传感器材料属性、工作环境、电子元器件和电路结构等的影响，会引入各种噪声，如电阻引起的热噪声、场效应管的沟道热噪声、光子噪声、暗电流噪声、光响应非均匀性噪声等。二是来源于图像信号传输过程中，如通过无线网络传输的图像会受到光或其他大气因素的干扰。由于传输介质和记录设备等的不完善，数字图像在其传输记录过程中往往会受到多种噪声的污染。另外，在图像处理的某些环节，当输入的对象并不如预想时也会在结果图像中引入噪声。
图像常见噪声基本上有4种，分别是高斯噪声、泊松噪声、乘性噪声和椒盐噪声，下面对这些噪声展开详细介绍。
6.2.3.1 高斯噪声
高斯噪声，顾名思义是指概率密度函数服从高斯分布(正态分布)的一类噪声，通常是因为不良照明和高温引起的传感器噪声。高斯噪声的概率密度函数为
式中:z——灰度值，z的值有70%落在[(μ－σ)，(μ＋σ)]范围内，有95%落在[(μ－2σ)，(μ＋2σ)]范围内；
μ——z的平均值或期望值；
σ——z的标准差，标准差的平方为z的方差；
p(z)——图像中灰度值为z的噪声点出现的频率。
添加高斯噪声前后的效果对比如图6－3所示。由图可知，通常在RGB图像中，高斯噪声显现更加明显。
图6－3 添加高斯噪声前后的效果对比(附彩插)
(a)RGB原图；(b)添加高斯噪声后的RGB图像；(c)灰度图原图；(d)添加高斯噪声后的灰度图
6.2.3.2 高斯白噪声
如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称为高斯白噪声，高斯白噪声的二阶矩不相关，一阶矩为常数，即先后信号在时间上具有相关性。
(1)白噪声在功率谱上(以频率为横轴，信号幅度的平方为功率)趋近为常值，也就是说这种噪声频率丰富，在整个频谱上都有成分，即从低频到高频的波都存在(低频指的是信号不变或缓慢变化，高频指的是信号突变)。高斯白噪声的功率谱密度服从均匀分布，利用MATLAB验证高斯白噪声的程序如下，实验结果如图6－4所示。
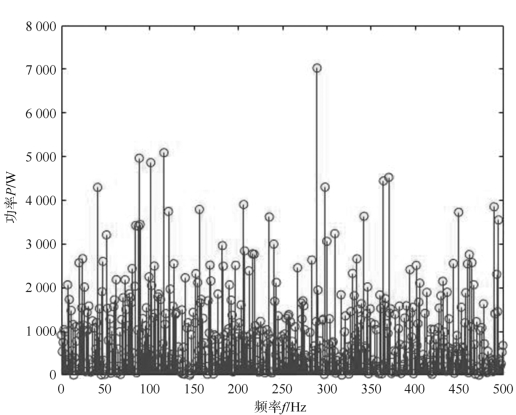
图6－4 高斯白噪声的功率谱密度
由图6－4可以看出，高斯白噪声的功率谱密度服从均匀分布。
(2)高斯白噪声具有相关性:某一时刻的噪声点都与其他时刻的噪声幅值有关。例如，此时刻的噪声幅值比上一时刻的大，而下一时刻的噪声幅值比此时刻的还大，即信号的幅值在时间轴上按从小到大的顺序排列。除此之外，幅值从大到小，或幅值一大一小等都称为“相关”，而非“随机”。
(3)从概率密度角度来说，高斯白噪声的幅度分布服从高斯分布，严格来说是高斯白噪声的瞬时值服从高斯分布。
6.2.3.3 泊松噪声
泊松噪声也称为散粒噪声，就是符合泊松分布的噪声模型，泊松分布适合描述单位时间内随机事件发生的次数的概率分布。例如，某一服务设施在一定时间内收到的服务请求的次数、电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等。
泊松噪声存在是因为光由离散的光子构成，即光的粒子性。光源发出的光子打在CMOS上，从而形成一个可见的光点，现在忽略光学元件和电路等，简化图如图6－5所示。光源每秒发射的光子到达CMOS的越多，则该像素的灰度值越大。但是，因为光源发射和CMOS接收之间都有可能存在一些因素导致单个光子并没有被CMOS接收到或者某一时间段内发射的光子特别多，所以这就导致了灰度值会有波动，也就是所谓的泊松噪声。(www.xing528.com)
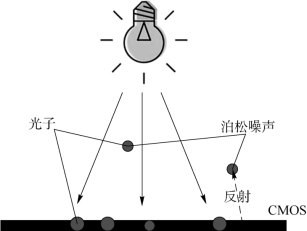
图6－5 泊松噪声形成过程简化图
在光源强度比较低的时候，如设定光强为每秒5个光子，那么CMOS每秒实际接收到的光子数为0～10，当然也可能会更多，但是概率几乎为0了，所以噪声最大为5。当光源强度比较高的时候，如每秒10 000个光子，那么CMOS每秒实际接收到的光子就可能为7 000～13 000(粗略的数字)，所以噪声最大为3 000。从这个例子可知，光源强度越高，噪声越大，这是泊松噪声的一个特点。
如图6－6所示，高斯噪声是与光强没有关系的噪声，无论光强是多少，噪声的平均水平(一般是0)不变；而泊松噪声，会随着光强的增大，平均噪声也增大。
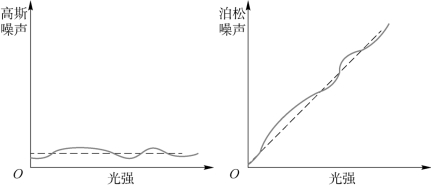
图6－6 高斯噪声和泊松噪声与光强之间的关系
泊松分布满足以下条件。
(1)时间越长，事件发生的可能越大，且不同时间内发生该事件的概率相互独立。
(2)对于非常短的一段时间Δt来说，事件发生的可能性为P(t，t＋Δt)＝λΔt＋o(Δt)。其中，P(t，t＋Δt)表示在Δt时间内事件发生的概率；λ为一个参数，代表单位时间(或单位面积)内随机事件的平均发生次数；o(Δt)为高阶无穷小。
(3)对于非常短的一段时间来说，出现该事件两次的概率几乎为0。
(4)事件发生的次数符合概率分布:P(X＝k)＝
(k＝0，1，2，…)。其中，X代表某一事件，k代表事件发生的次数，P(X＝k)代表该事件发生k次的概率，参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
对应到我们的光源成像在CMOS上面的事件则很明显:时间越长，有一个光子被CMOS接收到这个事件发生的可能性就越大，在非常短的时间内同时收到两个光子的可能性为零，经过一一对应，可发现泊松噪声是符合泊松分布的。
添加泊松噪声前后的效果对比如图6－7所示。由图6－3和图6－7的对比可知，添加高斯噪声的图像比添加泊松噪声的图像更加模糊。
图6－7 添加泊松噪声前后的效果对比(附彩插)
(a)RGB原图；(b)添加泊松噪声后的RGB图像；(c)灰度图原图；(d)添加泊松噪声后的灰度图
6.2.3.4 乘性噪声
乘性噪声是信道(信道即通信的通道，是信号传输的媒介)特性随机变化引起的噪声，它主要表现在无线电通信传输信道中。例如，电离层和对流层的随机变化引起信号不反应任何消息含义的随机变化，而构成对信号的干扰。乘性噪声只有在信号出现在上述信道中时才表现出来，它不会主动对信号形成干扰。乘性噪声普遍存在于现实世界的图像应用当中，如合成孔径雷达、超声波、激光等相干图像系统当中。添加乘性噪声前后的效果对比如图6－8所示，由图可知，添加乘性噪声时设置的方差越大，图像中噪声越多，图像退化越严重。
6.2.3.5 椒盐噪声
图6－8 添加乘性噪声前后的效果对比(附彩插)
(a)RGB原图；(b)添加方差默认值的乘性噪声后的RGB图像；(c)添加方差为0.2的乘性噪声后的RGB图像；(d)添加方差为10的乘性噪声后的RGB图像
椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是暗的区域有白色像素，或是两者皆有。椒盐噪声的成因可能是影像信号受到突如其来的强烈干扰，类比数位转换器或位元传输错误等。例如，失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。添加椒盐噪声前后的效果对比如图6－9所示，由图可知，噪声密度d越大，对图像的影响也就越大。
图6－9 添加椒盐噪声前后的效果对比(附彩插)
(a)RGB原图；(b)添加密度d＝0.05的椒盐噪声后的RGB图像；(c)添加密度d＝0.2的椒盐噪声后的RGB图像；(d)添加密度d＝0.5的椒盐噪声后的RGB图像
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
