同态滤波是把频域滤波和空域灰度变换结合起来的一种图像处理方法,它以图像的照度/反射率模型作为频域处理的基础,利用压缩亮度范围和增强对比度来改善图像的质量。这种方法可以使图像处理符合人眼对于亮度响应的非线性特性,避免了直接对图像进行傅里叶变换处理的失真。
一般来说,图像的边缘和噪声都对应于傅里叶变换的高频分量,而低频分量主要决定图像在平滑区域中总体灰度级的显示,故经过低通滤波处理的图像相比于原图像而言会少一些尖锐的细节部分;同样,经过高通滤波的图像在图像的平滑区域中将减少一些灰度级的变化并突出细节部分。因此,为了增强图像细节的同时尽量保留图像的低频分量,引入同态滤波,同态滤波可以在保留图像原貌的同时,对图像细节进行增强。在安防领域监控视频中有时会出现图像照明不均的问题,如果目标物体的灰度很暗,这样的图像灰度范围很大,无法辨认细节,如果采用线性灰度变换一般效果不大。若采用属于频域处理操作的同态滤波来解决上述问题则仅对图像较暗部分进行增强,其余部分依然保持原状。
一幅图像可看成由两部分组成,即
![]()
式中:i(x,y)——随空间位置不同的光强(Illumination)分量函数,其特点是缓慢变化,集中在图像的低频部分;
r(x,y)——景物反射到人眼的反射(Reflectance)分量函数,其特点是包含了景物各种信息,高频成分丰富。
同态滤波的基本原理是,将像素的灰度值看作是照度和反射率两个组分的产物,照度相对变化很小,可以看作是图像的低频成分,而反射率是高频成分,通过分别处理照度和反射率对像素的灰度值的影响,达到显示阴影区细节特征的目的。同态滤波分为以下5个基本步骤。
(1)对原图作对数变换,得到如下两个加性分量,即
![]()
(2)对数图像作傅里叶变换,得到其对应的频域表示为
![]()
(3)设计一个频域滤波器H(u,v),进行对数图像的频域滤波。
(4)傅里叶反变换,返回空域对数图像。
(5)取指数,得空域滤波结果。
综上,同态滤波的基本步骤如图5-25所示。
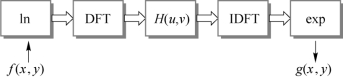
图5-25 同态滤波的基本步骤
式中:f(x,y)——原始图像;(https://www.xing528.com)
g(x,y)——处理后的图像;
ln——对数运算;
DFT——傅里叶变换(实际操作中运用快速傅里叶变换FFT);
IDFT——傅里叶反变换(实际常用快速傅里叶反变换IFFT代替);exp表示指数运算。
可以看出,同态滤波的关键在于频域滤波器H(u,v)的设计。对于一幅光照不均匀的图像,同态滤波可同时实现亮度调整和对比度提升,从而改善图像质量。为了压制低频的亮度分量,增强高频的反射分量,频域滤波器H(u,v)应是一个高通滤波器,但又不能完全消除低频分量,仅作适当压制。
因此,同态滤波器一般采用如下形式,即
![]()
其中,γL<1,γH>1,控制滤波器幅度的范围。Hhp(u,v)通常为高通滤波器,如高斯(Gaussian)高通滤波器、巴特沃斯(Butterworth)高通滤波器、Laplacian滤波器等。
如果Hhp(u,v)采用Gaussian高通滤波器,则
![]()
其中,c为一个常数,控制滤波器的形态,即从低频到高频过渡段的陡度(斜率),其值越大,斜坡带越陡峭,如图5-26所示。
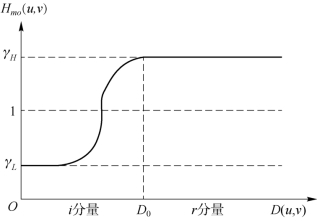
图5-26 同态滤波器的剖面
同态滤波前后的效果对比如图5-27所示,由图可知,同态滤波方法可以在增强图像高频信息的同时保留部分低频信息,达到压缩图像灰度的动态范围,增强图像对比度的效果。

图5-27 同态滤波前后的效果对比(附彩插)
(a)原始图像;(b)同态滤波增强后的图像
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




