低通滤波器的巴特沃斯方法及原理解析

图像在传递过程中，噪声主要集中在高频部分，为去除噪声改善图像质量，滤波器采用低通滤波器H(u，v)，来抑制高频成分，通过低频成分，然后再进行傅里叶反变换获得滤波图像，就可达到平滑图像的目的。在傅里叶变换域中，变换系数能反映某些图像的特征，如频谱的直流分量对应图像的平均亮度，噪声对应频率较高的区域，图像实体对应频率较低的区域等，因此频域常被用于图像增强。在图像增强中构造低通滤波器，使低频分量能够顺利通过，高频分量被有效地阻止，即可滤除该领域内噪声。由卷积定理，低通滤波器的数学表达式为

式中:F(u，v)——含有噪声的原图像的傅里叶变换域；

H(u，v)——传递函数；

G(u，v)——经低通滤波后输出图像的傅里叶变换。

假定噪声和信号成分在频率上可分离，且噪声表现为高频成分，那么低通滤波器可滤去高频成分，而低频信息基本无损失地通过。选择合适的传递函数H(u，v)对频域低通滤波关系重大。常用频域低通滤波器H(u，v)有4种，下面对这4种常用频域低通滤波器做详细介绍。

5.5.1.1　理想低通滤波器

设傅里叶平面上理想低通滤波器离开原点的截止频率为D0，则理想低通滤波器的传递函数为

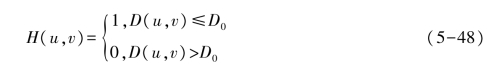
式中:H(u，v)——传递函数；

D(u，v)——点(u，v)到原点的距离，D(u，v)＝

D0——截止频率点到原点的距离。

图5－24中，在频域坐标系(u，v)中，D(u，v)表示点(u，v)到原点的距离，图中红色圆周上的点距离原点的距离为D0，进行理想低通过滤后，在圆周外面的将全部变暗(没有能量)。

图5－24　傅里叶变换(附彩插)

5.5.1.2　巴特沃斯(Butterworth)低通滤波器

n阶巴特沃斯低通滤波器的传递函数为(www.xing528.com)

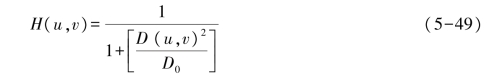
式中:H(u，v)——传递函数；

D(u，v)——点(u，v)到原点的距离，D(u，v)＝

D0——截止频率点到原点的距离。

5.5.1.3　指数低通滤波器

指数低通滤波器的传递函数为

式中:H(u，v)——传递函数；

D(u，v)——点(u，v)到原点的距离，D(u，v)＝

D0——截止频率点到原点的距离。

5.5.1.4　梯形低通滤波器

梯形低通滤波器的传递函数为

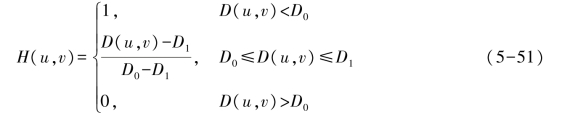
式中:H(u，v)——传递函数；

D(u，v)——点(u，v)到原点的距离，D(u，v)＝

D0，D1——截止频率点到原点的距离。