使用直方图进行数据处理

5.2.2.1　灰度直方图简介

灰度直方图是按照灰度值的大小，统计数字图像中的像素出现的频率，其横坐标是灰度级，纵坐标是该灰度出现的频率或像素的个数。灰度直方图能给出该图像的概括性描述，如图像中灰度的分布范围，整幅图像的亮暗程度以及对比度情况，但不能反映这些灰度在图像上的几何分布情况。灰度直方图分为3种类型，分别为单峰直方图、双峰直方图及多峰直方图。

单峰直方图:只有一个峰的直方图称为单峰直方图，如图5－4(b)所示，其对应的图像中对象区域只占很小部分比例。若洁净工件上有很小的疵点，则其直方图表现为单峰直方图，我们可利用单峰直方图分离疵点。

图5－4　单峰直方图

(a)原始图像；(b)图像对应直方图

双峰直方图:若图像可分为两部分，一部分是研究对象，另一部分是背景，那么图像会存在两个不同灰度的区域，其中对象对应直方图中的小峰，背景较亮区域对应于直方图中的大峰，如图5－5所示。

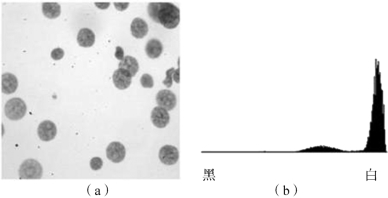
图5－5　双峰直方图

(a)原始图像；(b)图像对应直方图

多峰直方图:较复杂的图像一般对应多峰直方图，如图5－6所示。

直方图修正的目的是使修正后的图像的灰度间距拉开或者使图像灰度分布均匀，从而增大反差，使图像细节清晰，从而达到图像增强的目的，因此，直方图修正法也是图像增强的一个重要方法。直方图修正法主要包括直方图均衡化和直方图规定化两种。

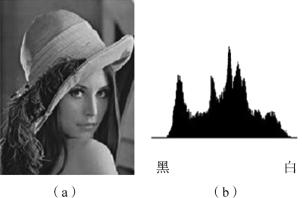
图5－6　多峰直方图

(a)原始图像；(b)图像对应直方图

5.2.2.2　直方图均衡化

直方图均衡化通过对原图像进行某种变换，使原图像的灰度直方图修正为均匀分布直方图，从而达到调整图像对比度的目的。通过这种方法，可以增加图像的全局对比度，使亮度更好地在直方图上分布。这种方法适用于背景和前景太亮或太暗的图像，如改善X光骨骼结构图像的明暗度，使得骨骼结构更加清晰。此方法优势在于技术成熟且操作可逆，若已知均衡化参数，则可恢复原始图像直方图，缺点在于可能会增加背景噪声对比度且降低信号对比度。图5－7为同一图像不同对比度与其对应的灰度直方图展示效果，由图可知，不同对比度的相同图像对应的灰度直方图差异巨大。

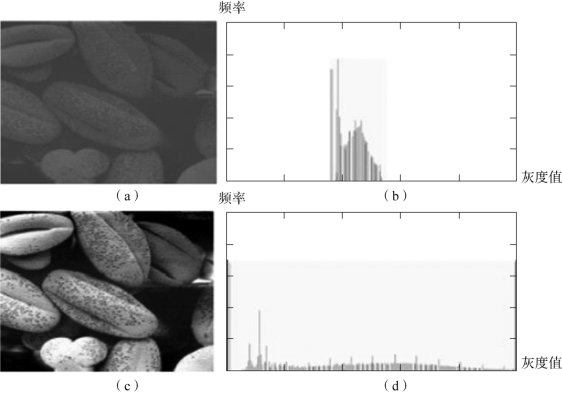
图5－7　同一图像不同对比度与其对应的灰度直方图展示效果

(a)低对比度图像；(b)低对比度图像对应的灰度直方图；(c)高对比度图像；(d)高对比度图像对应的灰度直方图

如果将图像中像素亮度(灰度级别)看成是一个随机变量，则其分布情况就反映了图像的统计特性，这可用概率密度函数(Probability Density Function，PDF)来刻画和描述，表现为灰度直方图。若要进行图像的直方图均衡化，必须首先求得均衡化函数。

为了便于分析，我们首先假设图像的灰度范围为0～1且连续，此时图像的归一化直方图即为概率密度函数，即

由概率密度函数的性质，有

设转换前图像的概率密度函数为pr(r)，转换后图像的概率密度函数为ps(s)，转换函数为s＝f(r)。由概率论知识可得

因此，若转换后图像的概率密度函数ps(s)＝1，0≤s≤1(即直方图是均匀的)，则必须满足

等式两边对r积分，可得

(www.xing528.com)

上式被称作图像的累积分布函数，其中μ仅代表求积分时使用的字母符号，无特殊含义。

式(5－8)是灰度取值在[0，1]范围内推导出来的，但在实际情况中，图像的灰度值范围为[0，255]，因此需将上式乘以最大灰度值Dmax(对于灰度图即为255)。此时，灰度均衡的转换公式为

式中:DB——转换后的灰度值；

DA——转换前的灰度值。

而对于离散灰度级，相应的转换公式为

式中:Hi——第i级灰度的像素个数；

A0——图像的面积，即像素总数。

需要注意的是，变换函数f是一个单调增加的函数，这是为了保证无论像素如何映射，图像原本的大小关系不变以及原图像较亮的区域依旧较亮，较暗的区域依旧较暗，图像只能发生对比度的变化，而绝对不能明暗颠倒。

5.2.2.3　直方图规定化

直方图规定化是使原图像灰度直方图变成规定形状的直方图而对图像作修正的增强方法。理想情况下，直方图均衡化实现了图像灰度的均衡分布，对提高图像对比度、亮度具有明显作用。在实际应用中，有时并不需要图像的直方图具有整体的均匀分布，而希望直方图与规定要求的直方图一致，这就需要用到直方图规定化，如图5－8所示。

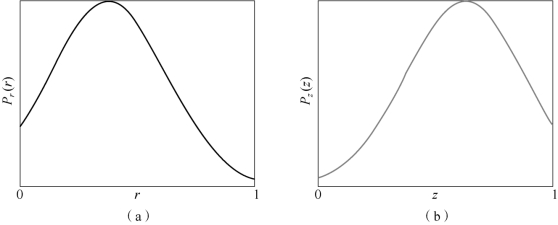
图5－8　直方图规定化

(a)原直方图；(b)规定直方图

设Pr(r)和Pz(z)分别表示原始灰度图像和目标图像的灰度分布概率密度函数，根据直方图规定化的特点与要求，应使原始图像的直方图具有Pz(z)所表示的形状，因此，建立Pr(r)和Pz(z)之间的关系是直方图规定化必须解决的问题。

根据直方图均衡化理论，首先对原始图像进行直方图均衡化处理，即求变换函数

现假定直方图规定化的目标图像已经实现，对于目标图像也采用同样的方法进行均衡化处理，因而有

式(5－12)的逆变换为

式(5－13)表明，可通过均衡化后的灰度级v求出目标函数的灰度级z。由于对目标图像和原始图像都进行了均衡化处理，因此具有相同的分布密度，即

因而可以用原始图像均衡化以后的灰度级s代表v，即

所以，可以依据原始图像均衡化后的图像的灰度值得到目标图像的灰度级z。

直方图增强处理也存在以下3点不足之处。

(1)处理后的图像灰度级有所减少，致使某些细节消失。

(2)某些图像(如直方图有高峰等)经处理后其对比度易产生不自然的过分增强。例如，某些卫星图像或医学图像因灰度分布过分集中，均衡化处理时其结果往往会出现过亮或过暗现象，达不到增强视觉效果的目的。

(3)对于图像的有限灰度级，量化误差经常引起信息丢失，导致一些敏感的边缘因与相邻像素点的合并而消失，这是直方图修正增强无法避免的问题。