监控视频中模糊视频帧的复原技术

4.6.3.1　运动模糊处理

图4－24是将监控视频中具有运动目标的某帧选取出来，并对该帧进行处理，得到有目标动作的区域。此外，将其运动方向按照图像退化的方法进行人为的模糊处理。这样做的目的是，减少其他没发生模糊的背景区域对频域变换后的特征的影响，达到明显的仿真模糊效果。图4－24(b)是彩图4－24(a)经过模糊步长为10，角度为0°(180°)处理得到的仿真图像。

图4－24　监控视频中运动模糊帧(附彩插)

(a)原视频帧；(b)运动模糊视频帧

4.6.3.2　基于运动模糊图像的频域分析算法

当监控视频中的移动物体与摄像头之间的相对位移速度过快时，虽然会导致图像帧出现运动模糊，但是运动模糊图像提供了运动目标的一些方向信息。本算法是将模糊运动图像进行傅里叶变换得到频域中的幅度谱图，再利用RADON变换将幅度谱上的平行条纹的方向进行提取，得到该图像可能的运动方向。因此，对于监控视频中存在的运动模糊视频帧，将该视频帧复原成清晰图像，读取视频帧的内容具有重要的研究意义。

MATLAB提供了fft函数和fft2函数。它们的作用分别是进行一维快速傅里叶变换和二维快速傅里叶变换。对应相反的ifft函数和ifft2函数分别是用于实现一维快速傅里叶反变换和二维快速傅里叶反变换的功能。

(1)fft2函数:灰度图像才能作为fft2函数的输入图像，函数的输出值为变换矩阵。傅里叶变换矩阵的变换系数是复数的形式，不能够直接显示，必须用abs函数进行求模以后才是傅里叶变换后的幅度谱。

(2)fftshift函数:fftshift函数的作用是将傅里叶变换得到的图像的幅度谱图进行平移变换，平移变换后的图像幅度谱中心，也就是矩阵的中心是从矩阵的原点平移过去的。图像中的能量大部分在低频部分，而图像的边缘信息在频谱的高频部分。在频谱中，白色区域代表了低频部分，能量高，主要是图像的内容信息，黑色区域代表高频部分，记录了图像的边缘信息。

图4－25为不同角度下的运动模糊图像，模糊角度分别为30°、90°、150°。分别对其进行傅里叶变换后得到的幅度谱如图4－26所示，可以看出垂直于模糊方向会在原点对应的两侧有平行的明暗条纹出现。幅度谱上对应的平行条纹会跟随运动方向变化，且条纹方向一直垂直于运动模糊的方向，最后利用RADON变换得到幅度谱对应的折线图准确地估算出图像的运动模糊方向，如图4－27所示。

图4－25　不同角度的运动模糊图像

(a)30°；(b)90°；(c)150°

图4－26　对应的频域幅度谱图

(a)30°；(b)90°；(c)150°(www.xing528.com)

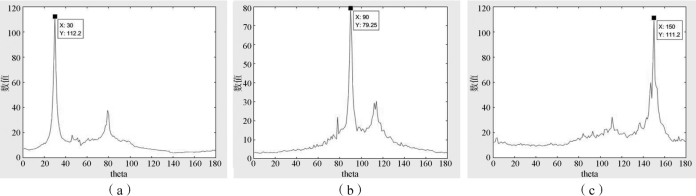
图4－27　对应的RADON变换折线图

(a)30°；(b)90°；(c)150°

为了能识别出上面运动模糊图像的幅度谱中明暗条纹的方向，在这里将条纹视为直线。对图4－26所示的幅度谱图像在0°～180°的角度范围内进行RADON变换，将对每个角度取RADON变换后的极大值作为该方向上的投影值，再在所有角度上取最大值对应的角度，作为运动模糊方向。图4－27是对图4－26中对应的幅度谱进行RADON变换后的折线图，x轴代表了角度，y轴代表了角度积分值。对图4－26的幅度谱进行中心化的操作后，水平和垂直方向存在明显的直线条纹干扰，所以在90°和180°有时可能会出现较大的峰值，但是在运动模糊方向的角度上也会有明显的峰值，且该峰值角度与运动模糊方向基本保持一致。

基于运动模糊图像的频域分析算法将图像复原成清晰图像的流程如图4－28所示。

图4－28　视频帧复原流程

图4－29(b)是将图4－24(b)进行频域变换后的幅度谱图像，可以看到仍然明显存在垂直于运动模糊角度的暗条纹，图4－29(c)是对图4－29(b)的幅度谱图像进行RADON变换的折线图，用来测量图像的模糊角度。经过上述实验中设置的参数与得到的折线中的参数对比可以看出，在折线中角度呈180°时为最大的峰值，计算出的角度与实际模糊运动方向是一致的，表明在频域中分析监控视频中的目标运动导致的模糊方向的方法是可取的。

图4－29　相同图像不同域空间展示(附彩插)

(a)运动模糊视频帧；(b)幅度谱图像；(c)RADON变换折线图

4.6.3.3　视频帧复原

将RADON变换得到的模糊方向角度作为点扩展函数的方向参数，并采用维纳滤波的方法对模糊图像进行复原。图4－30为不同信噪比下的复原图像，信噪比分别取值为0.01、0.001、0.000 1。从图4－30能够明显看出，不同信噪比下的复原效果是不同的，并且在信噪比为0.000 1时的模糊复原图像最清晰，效果最好。

图4－30　不同信噪比下视频帧复原图像(附彩插)

(a)信噪比0.01；(b)信噪比0.001；(c)信噪比0.000 1