前面章节已经讲解了傅里叶变换,但是傅里叶变换存在以下两点不足。
(1)傅里叶变换虽然能够很好地分析信号的频率信息,但是必须对一段信号(持续一段时间)进行分析才能得到较准的频率结果,因此对于非平稳信号(信号的频率会不断变化),只能得到这段时间内的频率分布,而并不能给出具体频率分量所在的时间。这就造成在时频上很不同的信号(频率上升和下降),傅里叶变换会得到相同的结果。
(2)为改善傅里叶变换对于时间的不敏感,提出了短时傅里叶变换(Short-Time Fouriev Transform,STFT),即将这段信号加窗分成多段信号分别进行傅里叶变换来对时间维分析结果进行改善。本质上,通过加窗STFT将大范围内的非平稳信号分割为多个小范围内的平稳信号,从而使得傅里叶变换能够对非平稳信号进行有效分析,但是其中涉及窗口大小的选择。如果窗口较大,时间分析的精度就会下降;如果窗口较小,频率分析的精度会下降。
由于傅里叶变换存在不足,因此提出了小波变换。小波变换(Wavelet Transform,WT)是一种新的变换分析方法,它继承和发展了短时傅里叶变换局部化的思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率改变的“时间-频率”窗口,是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征,能对时间(空间)频率进行局部化分析,通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了傅里叶变换的困难问题,成为继傅里叶变换之后在科学方法上的重大突破。
很多处理,包括压缩、滤波、图形处理等,其本质都是变换,那变换是什么东西呢?是基,也就是basis。简单来说,在线性代数里,basis是指空间里一系列线性独立的向量,而这个空间里的其他任何向量,都可以由这个向量的线性组合来表示。傅里叶展开的本质,就是把一个空间中的信号用该空间的某个basis的线性组合表示出来,小波变换也和basis有关。
小波直接把傅里叶变换的基换掉了——将无限长的三角函数基换成了有限长的会衰减的小波基,这样不仅能够获取频率,还可以定位到时间。这个基函数会伸缩、会平移(实质是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后,这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率的成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系,我们就知道信号包含该频率的成分的多少。小波的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基,如图4-9所示。

图4-9 长三角函数转换为衰减的小波基
小波公式为
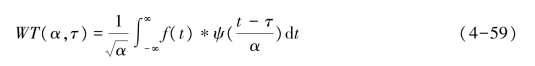
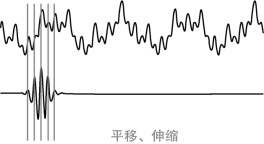
从式(4-59)可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度α和平移量τ。尺度α控制小波函数的伸缩,平移量τ控制小波函数的平移。尺度就对应于频率(反比),平移量τ就对应于时间,如图4-10所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图4-10 小波变换平移、伸缩图
当伸缩、平移到一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。有了小波,就可以做非稳定信号的时频分析。
小波变换有如下两个优点。
(1)解决了局部性,如图4-11所示。
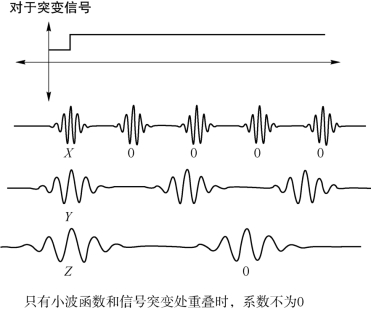
图4-11 小波变换解决局部性
(2)解决时频分析:做傅里叶变换只能得到一个频谱图,做小波变换却可以得到一个时频谱图,如图4-12所示。
小波变换可用于图像分解、去噪平滑以及边缘检测等,均有良好的实际应用效果。
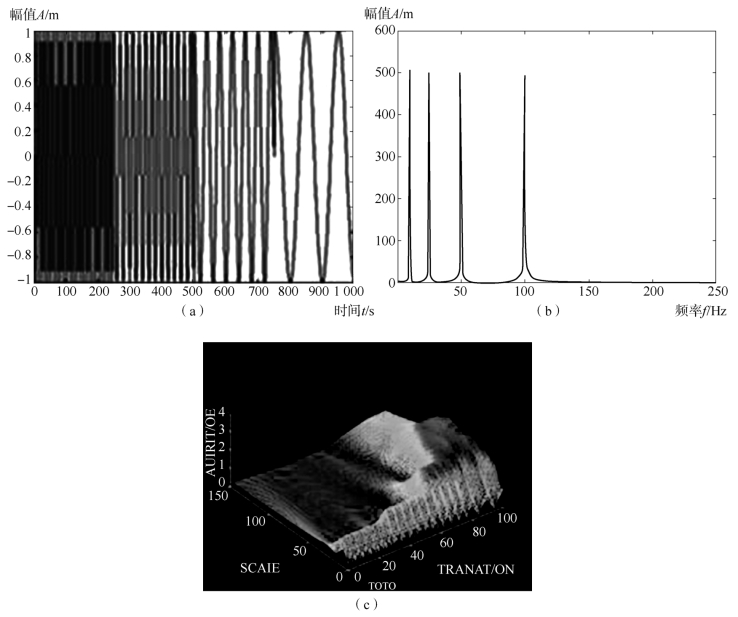
图4-12 不同图像变换对比
(a)原时域信号波形图;(b)傅里叶变换频谱图;(c)小波变换时频谱图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




