透视变换与几何变形的实现方法

3.2.3.1　透视变换

透视变换是把一个图像投影到一个新的视平面的过程，包括把一个二维坐标系转换为三维坐标系，然后把三维坐标系投影到新的二维坐标系。该过程是一个非线性变换过程，因此，一个平行四边形经过透视变换后只得到四边形，但不平行，但是透视变换能保持“直线性”，即原图像里面的直线，经透视变换后仍为直线。透视变换矩阵变换公式为

其中，透视变换矩阵为

要移动的点，即源目标点为

另外定点，即移动到的目标点为

以上是从二维空间变换到三维空间的转换，但图像在二维平面，故除以Z，(X′，Y′，Z′)表示图像上的点为

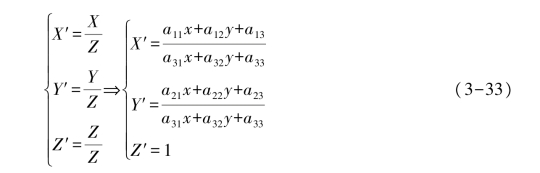
令a33＝1，展开上面公式，得到一个点的情况为

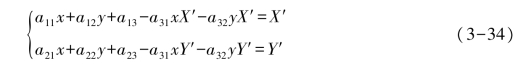(www.xing528.com)

透视变换过程中需要知道4个点之间的对应关系，因此由4个点可以得到以下8个方程，即可解出A。

图3－40是图像透视变换前后的效果对比。

图3－40　图像透视变换前后的效果对比

(a)原始图像；(b)透视变换后的图像

由于角度问题，某些证件照片难免会出现一些倾斜的问题，如图3－40(a)所示；透视变换要解决的就是通过一系列的操作，将倾斜的照片变得周正，如图3－40(b)所示。

3.2.3.2　几何变形

几何变形指原始图像上各个物体的几何位置、形状、尺寸、方位等特征产生变形。图3－41是几何变形(扭曲图像校正)前后的效果对比。

图3－41　图像几何变形(扭曲图像校正)前后的效果对比(附彩插)

(a)扭曲图像；(b)校正图像