3.2.2.1 图像缩放
图像缩放是将给定的图像在x轴方向按比例缩放fx倍，在y轴方向按比例缩放fy倍，从而获得一幅新的图像。图像缩放效果如图3－34所示。
若fx＝fy，则为全比例放缩；若fx≠fy，则产生几何畸变。
fx＝fy＝1/2是简单的图像比例缩小，此时图像被缩到原图的1/4倍，如图3－35所示。
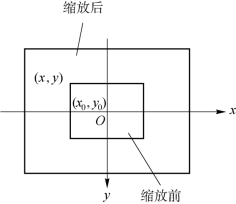
图3－34 图像缩放
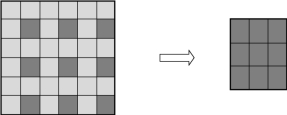
图3－35 图像被缩为原图像的1/4
fx＝fy＝2是简单的图像比例放大，此时图像被放大到原图的2倍，放大后图像(0，0)位置的像素值对应于原图(0，0)位置的像素值，(0，1)位置的像素值对应于原图中(0，0.5)位置的像素值，但(0，0.5)位置在图像中并不存在，这时应该怎么办呢?用插值方法解决即可，最简单的插值方法是，将原图中(0，0.5)位置的像素值近似为(0，0)位置的像素值，也可以近似为(0，1)位置的像素值，以此类推。此外，常用的插值方法有最近邻插值和双线性插值等，这两种插值方法将在6.4.2.2小节详细介绍。
图3－36是图像缩放前后的效果对比。
图3－36 图像缩放前后的效果对比
(a)原始图像；(b)缩小后的图像；(c)放大后的图像
由图3－36可知，随着图像放大倍数的增长，图像的清晰度会受到影响，图像放大倍数越大，图像就随之变得越来越模糊。
3.2.2.2 图像旋转
图像旋转属于图像位置变换，通常是以图像的中心为原点，将图像上的所有像素都旋转一个相同的角度，旋转后，图像的大小一般会改变。图像旋转θ角示意如图3－37所示。
(www.xing528.com)
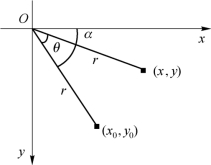
图3－37 图像旋转θ角示意
由图3－37可知，假设图像旋转θ角，原图像的坐标点(x0，y0)对应旋转后图像的坐标点(x，y)，那么
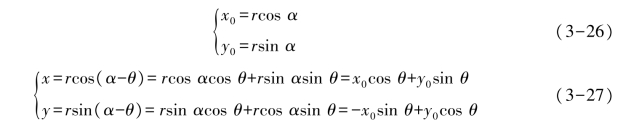
则旋转后图像的坐标点与原图像的坐标点之间的关系为
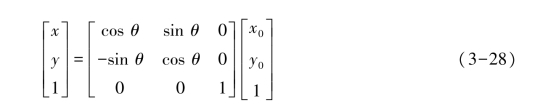
式中:θ——图像逆时针旋转的角度。
图3－38是图像旋转前后的效果对比。
图3－38 图像旋转前后的效果对比
(a)原始图像；(b)旋转后的图像
3.2.2.3 图像剪切
在进行图像处理的过程中，有时候用户只对采集图像的部分区域感兴趣，这时候就需要对原始图像进行剪切。MATLAB的IPT提供了函数imcrop()进行图像的剪切，下面用一段简短的程序及其运行结果(见图3－39)向大家展示图像剪切操作。
图3－39 图像剪切操作
(a)选取图像剪切区域；(b)图像剪切结果展示
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
