图像的数据结构和表示

2.2.2.1　图像的表示

对一幅图像f(x，y)采样后，可得到一幅M行、N列的图像，我们称这幅图像的大小是M×N，相应的值是离散的。为了符号清晰和方便可见，这些离散的坐标都取整数。这里介绍两种方法表示数字图像。

一种是将图像的原点定义为(x，y)＝(0，0)，图像第1行的下一坐标点为(x，y)＝(0，1)，坐标(0，1)用来表示沿着第1行的第2个取样。图2－18显示这一坐标约定，注意x是从0～(M－1)的整数，y是从0～(N－1)的整数。

另外一种是规定坐标原点为(x，y)＝(1，1)，如在MATLAB的图像处理工具箱中就使用这种图像规定格式，这种约定如图2－19所示。

图2－18　图像的表示1

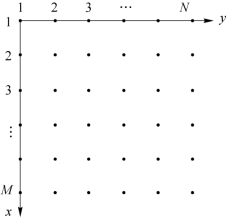
图2－19　图像的表示2

根据图2－18所示的坐标系统，我们可以得到数字图像的下列表示:

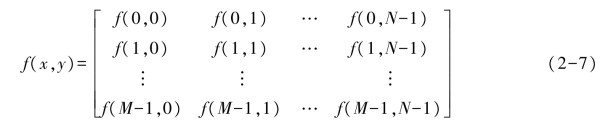
式(2－7)右边是定义的一幅数字图像，阵列中每个元素都被称为图像元素、图画元素或像素。以后，我们用图像和像素这两个术语表示数字图像及元素。

按照图2－19所示的坐标系统可将数字图像表示成MATLAB矩阵:

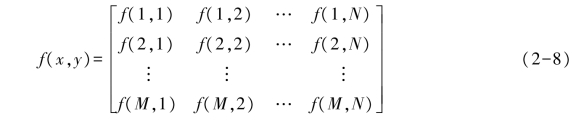
此处需要详细解释一些概念，在模拟图像中，(x，y)代表图像上某点的空间位置，f(x，y)代表(x，y)点处图像的灰度值；在数字图像中，(x，y)代表数字图像上某像素所在的行列位置，f(x，y)代表像素点处的灰度值，一般是一个整数。

2.2.2.2　图像的类型

MATLAB工具箱支持4种图像类型，分别是二值图像、灰度图像、RGB图像、索引图像，下面对这4种图像类型依次展开详细介绍。

二值图像经常使用位图格式存储，通常用一个二维数组来描述，并以1位表示一个像素，组成图像的像素值非0即1，没有中间值，通常0表示黑色，1表示白色，如图2－20所示。在MATLAB中用一个由0和1组成的二维逻辑矩阵表示，二值图像的优点是描述文字或者图形占用空间少，缺点是只能描述人物或风景图像的轮廓信息。

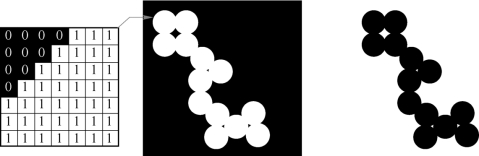
图2－20　二进制图像

灰度图像也称为单色图像，通常由一个二维数组表示，并以8位表示一个像素，通常0表示黑色，255表示白色，1～254表示不同的深浅灰色，如图2－21所示。在MATLAB中，灰度图像可以用不同的数据类型表示，只需保证每个像素能在一定的范围内取值即可，若使用8位无符号整数表示，则其取值范围是[0，255]；若使用16位无符号整数表示，则其取值范围是[0，65 535]；若使用双精度表示，则其取值范围是[0，1]。

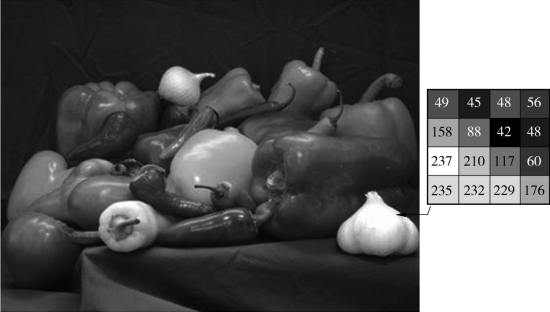
图2－21　灰度图像

RGB图像如图2－22所示，利用3个分别代表R、G、B分量的大小相同的二维数组表示图像中的像素，通过3种基本颜色可以合成任意颜色。每个像素中的每种颜色分量占8位，由[0，255]中的任意数值表示，那么一个像素就由24位表示。在MATLAB中，RGB图像存储为M×N×3的多维数据矩阵，其中元素可为3种数据类型，同灰度图像。

图2－22　RGB图像(附彩插)

(a)RGB值；(b)图像

索引图像包含一个数据矩阵X和一个颜色映射(调色板)矩阵map，如图2－23所示。颜色映射矩阵map是一个N×3的数据矩阵，其中每个元素都是位于[0，1]之间的double类型，map矩阵每一行有3列，分别表示红色(R)、绿色(G)和蓝色(B)。图像中每个像素的颜色通过X的像素值作为map的下标来获得。例如，X中的元素1指向map中的第1行所有元素，10指向map中的第10行所有元素。调色板与索引图像通常存储在一起，并一起自动装载。(www.xing528.com)

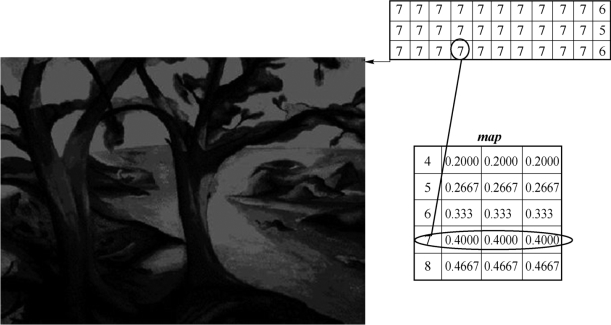
图2－23　索引图像

2.2.2.3　图像的数据结构

图像的数据结构用于目标表示和描述，数字图像处理中常用的数据结构有矩阵、链码、拓扑结构和关系结构。

(1)矩阵用于描述图像，可以表示黑白图像、灰度图像和彩色图像，矩阵中的一个元素表示图像的一个像素。

矩阵描述黑白图像时，矩阵中的元素取值只有0和1两个值，如图2－24所示，因此黑白图像又称为二值图像。

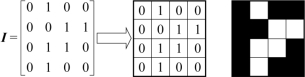
图2－24　黑白图像的矩阵描述

矩阵描述灰度图像时，矩阵中的元素由一个量化的灰度级描述，灰度级通常为8位，即0到255之间的整数，其中0表示黑色，255表示白色，如图2－25所示。

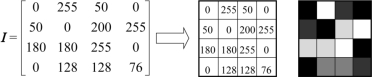
图2－25　灰度图像的矩阵描述

矩阵描述彩色图像时，彩色图像的每个像素都是由不同灰度级的红、绿、蓝描述的，利用3个分别代表R、G、B分量的大小相同的二维数组表示图像中的像素，R表示红色，G表示绿色，B表示蓝色，通过3种基本颜色可以合成任意颜色，如图2－26所示。

图2－26　彩色图像的矩阵描述

(2)链码用于描述目标图像的边界，通过规定链的起始坐标和链起始坐标的斜率，即可用一小段线段来表示图像中的曲线。因为链码表示图像边界时只需标记起点坐标，其余点用线段的方向数代表方向即可，这种表示方法节省了大量的存储空间。常用的链码按照中心像素点邻接方向个数的不同，分为4连通链码和8连通链码，如图2－27所示。4连通链码的邻接点有4个，分别在中心点的上、下、左和右；8连通链码比4连通链码增加了4个斜方向，因为任意一个像素周围均有8个邻接点，而8连通链码正好与像素点的实际情况相符，能够准确地描述中心像素点与其邻接点的信息，所以8连通链码的使用相对较多。

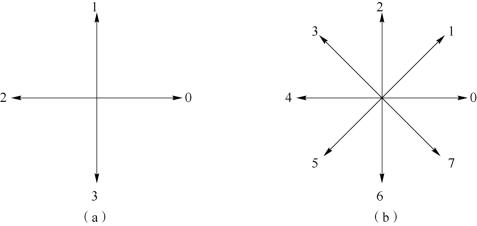
图2－27　链码

(a)4连通链码；(b)8连通链码

为了实现链码与起始点无关，需要将链码归一化。最简单的方法是将链码看成一个自然数，其中最小的自然数即为归一化结果。如图2－28所示，链码归一化结果为07107655533321。

(3)拓扑结构用于描述图像的基本结构，通常用于形态学或二值图像的图像处理当中。拓扑结构在图像中定义相邻的概念，一个像素与它周围的像素组成一个邻域，像素点p周围有8个相邻的像素点，若只考虑上下左右则有4个像素点则称4邻域，若只考虑对角上的4个像素点则称为对角邻域，4邻域和对角邻域都加上称为8邻域。相关内容在3.1.1小节有详细介绍。

图2－28　链码

(4)关系结构用于描述一组目标物体之间的相互关系，常用的描述方法为串描述和树描述，如图2－29所示。串描述是一种一维结构，当用串描述图像时，需要建立一种合适的映射关系，将二维图像降为一维形式，串描述适用于那些可以从头到尾连接或某些连续形式的图像元素的描述，链码表示就是基于串描述思想的。树描述是一种能够对不连接区域进行很好描述的方法。在树图中有两类重要信息:一个是关于节点的信息，另一个是节点与其相邻节点的关系信息。第一类信息表示目标物体的结构，第二类信息表示一个目标物体和另一个目标物体的关系。树是一个或一个以上节点的有限集合，其中，有一个唯一指定的节点为根，剩下的节点划分为多个互不连接的集合，这些集合称为子树，树的末梢节点称为叶子。

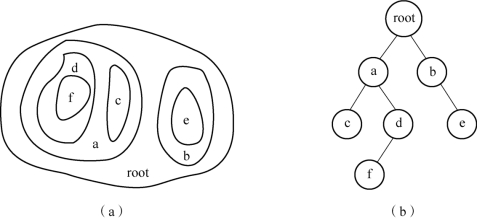
图2－29　串描述和树描述

(a)串描述；(b)树描述