试验数据整理和分析技巧

桥梁结构的动力特性(如结构的固有频率、阻尼系数和振型等)只与结构本身的固有性质有关(如结构的组成形式、刚度、质量分布和材料的性质等),而与荷载等其他条件无关。 结构的动力特性是结构振动系统的基本特性,是进行结构动力分析所必需的参数。

对于比较简单的结构,一般只需结构的一阶频率;对于较复杂的结构动力分析,还应考虑第二、第三甚至更高阶的固有频率及相应的振型。 至于系统的阻尼特性只能通过试验的方法确定。

1)结构固有频率

按照前面叙述的激振方法,使桥梁产生的自由振动,通过测试系统实测记录结构的衰减振动波形,如图10.2 所示。 在记录的振动波形曲线上,可根据时标符号直接计算出结构的固有频率f0:

式中　L——两个时标符号间的距离,mm;

n——波数;

S——n 个波长的距离,mm;

t1——时标的间隔(常用1 s,0.1 s,0.01 s 3 种标定值)。

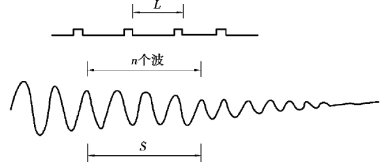
图10.2　由衰减振动曲线求固有频率

在计算频率时,为消除冲击荷载的影响,开始的一二个波形应舍弃,从第三个波形开始计算分析。

当使用激振器时,结构产生连续的周期性强迫振动,在激振器振动频率与结构的固有频率一致时,结构出现共振现象,振幅达到最大值,共振波峰处的频率即为结构的固有频率,如图10.3 所示。

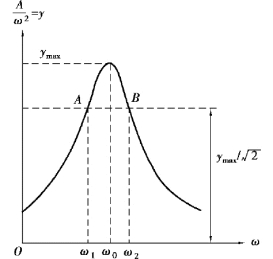
图10.3　共振曲线

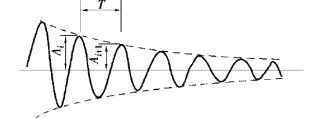
图10.4　由衰减振动曲线求阻尼特性

2)结构阻尼

桥梁结构的阻尼特性,一般用对数衰减率δ 或阻尼比D 来表示。 实测的振动衰减曲线如图10.4 所示,由振动理论知,对数衰减率为:

式中　Ai,Ai+1——相邻两个波的振幅值,可直接从衰减曲线上量取。

实践中,常从衰减曲线上量取m 个波形,求得平均的衰减率:

由振动理论知,对数衰减率δ 与阻尼比D 的关系为:

对于一般材料的阻尼比都很小,因此:

在实测的共振曲线上也可推算阻尼比,如图10.3 所示。 具体做法是取ymax/ 2 值作一水平线,同曲线相交于A,B 两点,其对应的横坐标为ω1,ω2。

式中　ω0——结构的固有频率。

3)振型

结构的振型是结构相应于各阶固有频率的振动形式,一个振动系统振型的数目与其自由度数目相等。 桥梁结构是一个具有连续分布质量的体系。 也就是说,桥梁是一无限多自由度体系,因此,其固有频率及相应的振型也有无限多个。 但是,对于一般的桥梁结构,第一固有频率即基频,对结构的动力分析才是重要的。 对于较复杂的动力分析问题,也仅需分析前面几个固有频率。 也就是说,通常情况下,一般低阶振型才是重要的。 图10.5 表示具有分布质量的各种梁的振型。

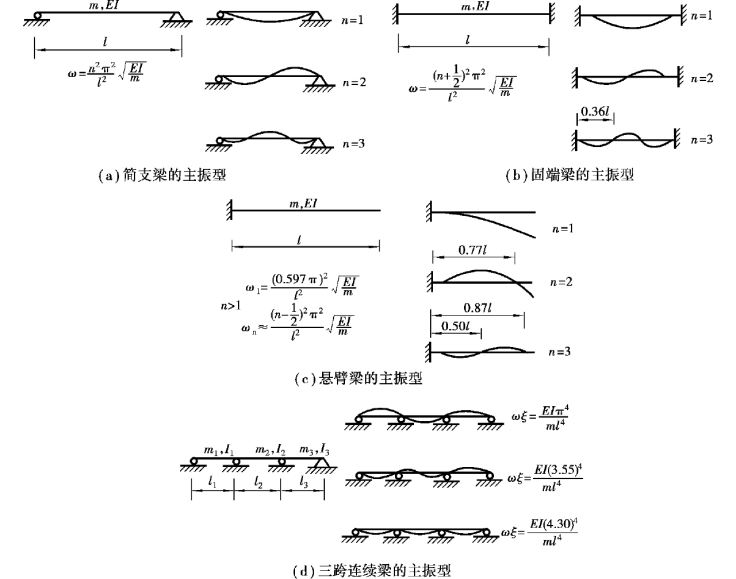
图10.5　具有分布质量的各种梁的振型(www.xing528.com)

采用共振法测定振型时,将若干传感器安装在结构各有关部位。 当激振装置激发结构共振时,同时记录结构各部位的振幅和相比,比较各测点的振幅及相位便可绘出振型曲线。

传感器的测点布置视结构形式而定,一般要根据理论分析,估计振型的大致形状,然后在变位较大的部位布点,以便能较好地连接出振型曲线。

振型的测定一般采用两种方法:一是在结构上同时安装许多传感器,这时必须保证预先要精确标定所有传感器的灵敏度,在用多路放大器时,还要求放大器的特性相同;另一种方法只用一个传感器,测试时要不断改变它的位置,以便测出各点的振幅。 这种方法需要对传感器多次拆卸和安装,并且还需要有一个作用参考点不能移动的传感器,各次测定值均应同参考点对应比较。

4)结构动力响应

在动力荷载作用下,桥梁结构某些部位的振动参数(如振幅、频率、位移、应力等)的测定,可根据试验的具体要求和结构的形式布置测点,采用适当的仪表进行测试。 动力荷载作用于结构上产生的动挠度,一般较同样的静荷载所产生的相应静挠度要大。 动挠度与静挠度的比值称为活荷载冲击系数。 由于挠度反映了桥跨结构的整体变形,是衡量结构刚度的主要指标,因此,活荷载冲击系数综合反映了荷载对桥梁的动力作用。 活荷载冲击系数与结构的形式、车辆运行速度和桥面的平整度等有关。

为了测定冲击系数,应使车辆荷载以不同的速度驶过桥梁,并逐次记录跨中挠度的时历曲线,如图10.6 所示。 按冲击系数的定义有:

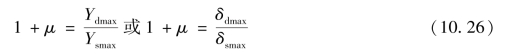
式中　Ydmax——最大动挠度值;

Ysmax——最大静挠度值。

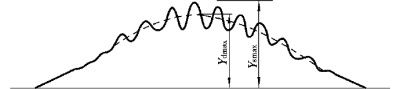
图10.6　移动荷载作用下结构变形曲线

若对所有局部“波谷”动响应值与相应“静”载作用下该点响应值之比计算得到的冲击系数进行加权处理,可得到如下冲击系数计算式:

式中　Ymaxi——车辆荷载过桥时动挠度或动应变时程曲线上的一个“波谷”值;

Ymini——与Ymaxi相应的“波峰”动响应值;

Ymeani——相应的“静”载作用下该点的响应值;

μi——“波谷”处所对应的局部冲击系数;

αi——权重。

该方法虽然计算较为复杂,但可真实反映车辆的全程冲击作用。

5)资料整理与判定

分析计算和资料整理应包括下列内容:

①动载试验荷载效率。

②各试验工况下动挠度、动应变、加速度等的时域统计特性,包括最大值、最小值、均值和方差等。

③典型工况下主要测点的实测时程曲线。

④典型的自振频谱图。

⑤实测自振频率与计算频率列表比较。

⑥冲击系数-车速相关曲线图或列表。

⑦其他必要的图表、曲线、照片等数据或资料。

桥梁结构性能分析通过下列方法进行:

①比较实测自振频率与计算频率,实测频率大于计算频率时,可认为结构实际刚度大于理论刚度,反之则实际刚度偏小。

②比较自振频率、振型及阻尼比的实测值与计算数据或历史数据,可根据其变化规律初步判断桥梁技术状况是否发生变化。

③比较实测冲击系数与设计所用的冲击系数,实测值大于设计值时应分析原因。

自振频率与结构刚度有着明确的关系。 自振频率容易精确测量,利用自振频率评价桥梁的刚度也具有较高的可靠性。 结构部件出现缺损时,一般自振频率会降低,振型出现变异。桥梁结构存在或出现缺损时,一般会造成振型的变异。 一般来讲,变异区段即为缺损所在区段。 阻尼比参数,可以通过和同一座桥的历史数据对比,或同类桥梁历史经验数据对比,粗略判断桥梁结构的技术状况是否出现劣化,如阻尼比明显偏大,则桥梁结构技术状况可能存在缺损或出现劣化。