深入了解溶液的基本概念，

在吸收式制冷系统中，通常用两种不同挥发性物质组成的二元溶液工质。如吸收式制冷循环中的氨水溶液或溴化锂水溶液，均属于二元溶液。

二元溶液与纯物质之间存在着很大差别。纯物质各相的成分始终相同，在相变过程中，例如汽化过程，压力和温度始终保持不变，即t_s=f（p_s）。二元溶液就不一样了，不仅处于平衡的液相和气相成分不一样，而且在相变时，如定压下的汽化过程，温度也不能保持恒定，而是不断升高。

1.质量分数和摩尔分数

一种组分的质量与溶液质量之比称为这种组分的质量分数。当溶液仅由组分1和组分2所组成时，则组分1的质量分数ξ₁为

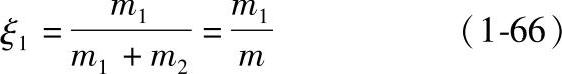
式中 m₁、m₂、m——溶液中组分1、组分2及溶液的质量。

显然，组分2的质量分数ξ₂为

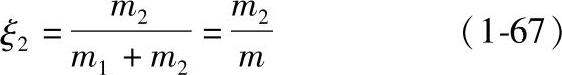
因此 ξ₁+ξ₂=1 （1-68）

如组分1的相对分子质量为M₁，组分2的相对分子质量为M₂，则组分1及组分2的摩尔数分别为

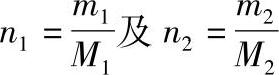
溶液的摩尔数为

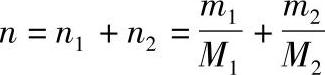
由此得组分1及组分2的摩尔分数x₁及x₂分别为因此

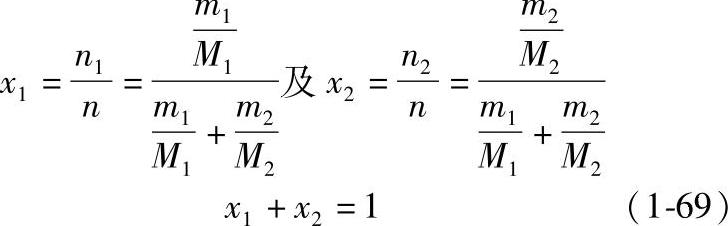
2.理想溶液

在一定温度和压力下，溶液中任何一种物质在任何质量分数下，均遵守拉乌尔定律的溶液，称为理想溶液。理想溶液的各种组分，在量上无论按什么比例，均能彼此均匀相溶；溶液中各种物质分子之间的相互吸引力完全相同，即溶剂分子之间、溶质分子之间及溶剂与溶质分子之间的相互吸引力完全相同；两种溶体相溶时无热效应；在相溶过程中容积无变化。

与理想气体相似，理想溶液也是一个极限概念，只有将溶液的质量分数尽量减小（即溶质的含量极少），成为稀溶液时，其性质才接近理想溶液。

3.拉乌尔定律(www.xing528.com)

拉乌尔定律说明，理想溶液中组分i的蒸汽分压力等于在溶液相同温度下，纯物质i的饱和蒸汽压和组分i的摩尔分数的乘积。其数学表达式为

式中 p_i——组分i的蒸汽分压力（Pa）；

p⁰_i——在溶液相同温度下，组分i单独存在时的饱和蒸汽压力（Pa）；

x_i——组分i在溶液中的摩尔分数。

根据拉乌尔定律，对由物质A和物质B所组成的二元溶液，可得

p_A=p⁰_Ax_A及p_B=p⁰_Bx_B

则二元溶液的总压力为

p=p_A+p_B=p⁰_Ax_A+p⁰_Bx_B

因为x_A=1-x_B，所以上式可写成

p=p⁰_A+（p⁰_B-p⁰_A）x_B （1-71）

式（1-71）为一直线方程，如图1-33所示。如果两种液体混合成一理想溶液，则溶液的总蒸汽压力在两纯液体的饱和蒸汽压力之间。图1-33也称为压力-摩尔分数图。

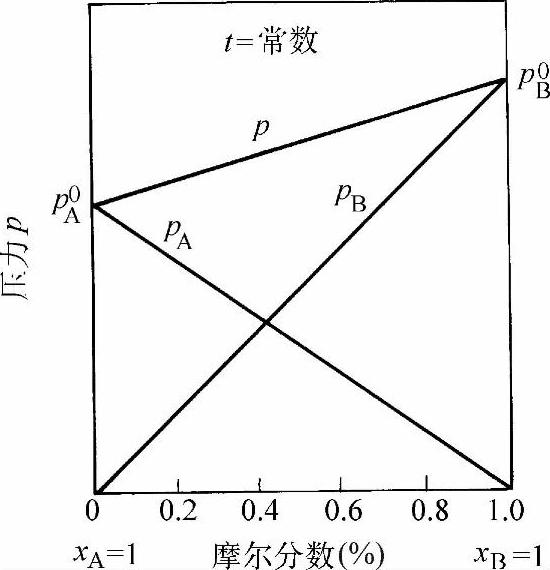
图1-33 理想溶液中蒸汽总压力和分压力的关系

图1-34表示溶液摩尔分数与蒸汽摩尔分数之间的关系。由于易挥发的组分B在蒸汽中的摩尔分数，一定大于溶液中的摩尔分数，所以蒸汽摩尔分数曲线（虚线）一定在溶液摩尔分数直线的下面。例如：当溶液的摩尔分数为x′_B时，溶液中总蒸汽压力点C所对应的蒸汽点D的摩尔分数为x″_B，显然x″_B＞x′_B。

应该指出：大多数溶液不具有理想溶液的性质，实际溶液中各组分的蒸汽分压力在应用拉乌尔定律时，将产生偏差。但理想溶液的概念不仅在理论上有价值，而且也有实际意义，只要对理想溶液的公式作必要的修正，就能应用于实际溶液中。

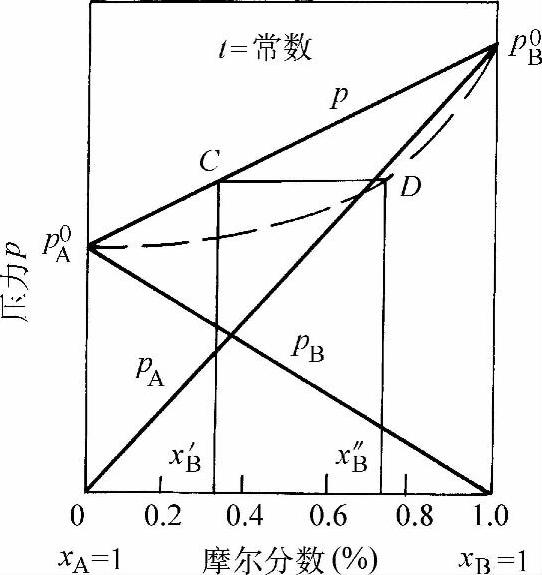
图1-34 溶液与蒸汽摩尔分数的关系