热力学第二定律与比熵的解析

1.热力学第二定律

热力学第一定律确定了热能传递、热能与机械能相互转换过程中的数量守恒关系。但人类通过长期的实践发现，并不是任何不违反热力学第一定律的过程都是可以实现的。因为自然界的一切过程都具有方向性，而热力学第二定律则阐述了自发过程进行的方向性和它的不可逆性，以及研究非自发过程必须具备的补充条件。

热力学第二定律有多种表述方式，但归纳起来主要有以下两种。

（1）克劳休斯表述法 热量不可能自发地、不付代价地从低温物体传到高温物体。它阐述了热量传递方向，即热量总是自发地、没有任何限制地从高温物体传到低温物体，正如水总是自发地、没有限制地从高水位流向低水位一样。若要使低温物体的热量传向高温物体，如制冷过程，则必须消耗一定的能量后才能实现。这与低水位的水流向高水位时，必须通过水泵消耗一定能量才能实现一样，消耗能量的过程就是一个补充条件。

（2）开尔文-普朗克表述法 不可能制造出只从一个热源取得热量，使之完全变成机械能而不引起其他变化的循环发动机。

从上述说明可以知道，热功间的相互转换必然会有能量损失，因此，研究热力循环时提高热效率是一项重要任务。

2.热力循环和热效率

如图1-5所示，工质从某一初态1出发，经过一系列状态变化后，又回复到初态1的封闭热力过程，称为热力循环或简称循环。根据循环所产生的不同效果，可分为正循环（或称动力循环）和逆循环（或称制冷循环）。

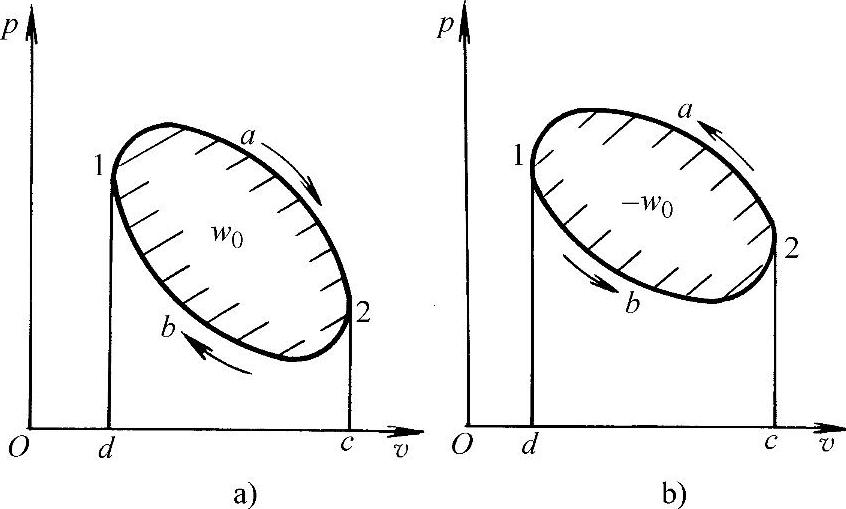
图1-5 热力循环

a）正循环 b）逆循环

正循环是把热能转换为机械能的循环，如图1-5a所示。所有热力发动机都是正循环，按顺时针方向进行。正循环对外所作之净功w₀为膨胀功与压缩功之差，在p-v图上为循环曲线所包围的面积1a2b1（正值）。正循环所获得的净功为

w₀=q₁-q₂ （1-18）

式中 q₁——工质从高温热源吸进的热量；

q₂——工质向低温热源放出的热量。

衡量正循环的经济性，通常用循环热效率η_t评介。循环热效率定义为工质在整个热力循环中，对外界所作的净功w₀与循环过程中外界给工质的热量q₁的比值，即

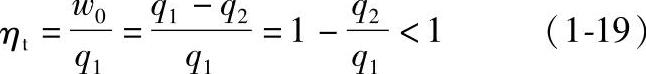
大量实践证明，提高高温热源温度，降低低温热源温度，热机的热效率越高。若热源为恒温热源，高温热源的温度为T₁，低温热源的温度为T₂，则热效率也可表示为

(www.xing528.com)

逆循环是消耗一定量的机械能，迫使高温热源的热量流向低温热源的循环。压缩式制冷及热泵供热都是利用逆循环工作的，如图1-5b所示。该循环按逆时针方向进行。工质从低温热源吸进的热量为q₂，向高温热源放出的热量为q₁，逆循环所消耗的净功w₀为循环曲线所包围的面积1b2a1（负值）。

根据热力学第一定律，可将逆循环消耗的净功为

-w₀=q₂-q₁或q₁=q₂+w₀ （1-21）

当逆循环为制冷循环时，衡量该循环的经济性采用制冷系数，其定义为

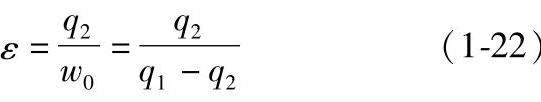
当逆循环为热泵循环时，衡量该循环的经济性采用供热系数，其定义为

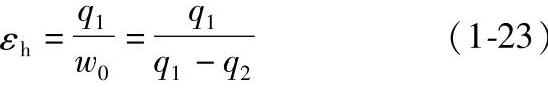
由式（1-22）可知，制冷系数ε可大于1，也可以等于1或小于1。而式（1-23）表示的供热系数ε_h总大于1，即该循环过程向外界放出的热量总大于消耗的功。

3.比熵及温熵图

比熵是表征工质状态变化时，与外界换热程度的一个导出热力状态参数。对于单位质量工质，称为比熵，用符号s表示，单位为kJ/（kg·K）。与焓一样，熵的绝对值也无法确定，只需知道工质状态变化时熵的变化情况，即用其相对值。单位质量工质在等温加热过程中，从外界加入热量q，加热时的温度为T，加热前后工质的熵分别为s₁和s₂，对于可逆过程可得

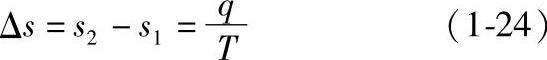
或 q=T（s₂-s₁） （1-25）

当s₂＞s₁时，q＞0，表示工质从外界吸收热量；当s₂＜s₁时，q＜0，表示工质对外界放出热量；当s₂=s₁时，表示等熵过程，或称绝热过程，工质与外界无热量交换。

熵在制冷循环的分析和计算中具有极重要的意义。例如，要把热量由低温物体传到高温物体，这是一个非自发过程，要使这一过程得以实现，必须辅以能量补偿，以使系统总的熵增加。

类比于p-v图，以热力学温度T为纵坐标，比熵s为横坐标组成的温-熵（T-s）图，如图1-6所示。与p-v图一样，图中每一条曲线可代表一个可逆过程。温-熵图中过程曲线1—a—2下面的面积1a2s₂s₁1，表示该过程中工质与外界所传递的热量，因此T-s图又称为示热图。在制冷技术中，T-s图具有重要的实用价值。

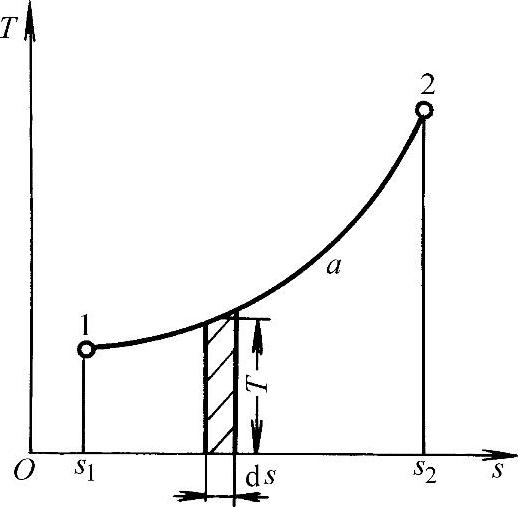
图1-6 温-熵图