单级放大电路频率响应优化

1.频率响应的基本概念

前面分析放大电路时，忽略了电路中电抗性器件电容的影响，而且在分析电路时，只考虑到单一频率的正弦输入信号。实际上，放大电路中存在电抗性器件电容，如外接的隔直耦合电容、三极管的极间电容、线间的杂散电容等。这些电容对不同频率的信号会产生不同的影响，呈现的阻抗有大有小。另外，实际放大电路的输入信号非常复杂，不仅仅是单一频率的正弦信号，而是一段频率范围（频段）。因此在考虑到这些因素后，放大电路的放大倍数对于不同频率的信号会有所变化。这种放大倍数随信号频率变化的关系称为放大电路的频率特性，也称为频率响应。频率响应包含幅频响应和相频响应两部分。

因为讨论涉及相位，这里用复数表示信号。

用关系式来描述放大电路的电压放大倍数与信号频率的关系。其中Au（f）表示电压放大倍数的模与信号频率的关系，称为幅频响应；φ（f）表示放大电路的输出电压与输入电压的相位差与信号频率的关系，称为相频响应。

2.上、下限频率和通频带

图2.64所示为阻容耦合放大电路的幅频响应。从图中可以看出，在某一段频率范围内，放大电路的电压增益与频率f无关，是一个常数，这时对应的增益称为中频增益Aum；但随着信号频率的减小或增加，电压放大倍数明显减小。

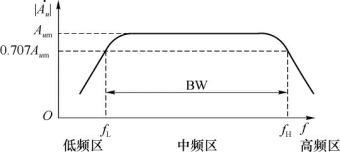
图2.64　阻容耦合放大电路的幅频响应

（1）下限频率fL和上限频率fH：当放大电路的放大倍数下降到0.707Aum时，所对应的两个频率分别称为放大电路的下限频率fL和上限频率fH。

（2）通频带BW：fL和fH之间的频率范围称为放大电路的通频带，用BW表示，即

一个放大器的通频带越宽，表示其工作的频率范围越宽，频率响应越好。

3.单级共射放大电路的频率响应

根据放大电路的上、下限频率及通频带，在分析放大电路的频率特性时，常把频率范围划分为3个频区：低频区、中频区和高频区。下面就结合图2.65所示的单级阻容耦合基本共射放大电路来分析单级放大电路的频率响应。

（1）中频区。若信号的频率在下限频率fL和上限频率fH之间，称此频率区域为中频区。在中频区，忽略所有电容的影响，视隔直耦合电容和旁路电容为交流短路，视极间电容和杂散电容为交流开路。这种情况与我们之前的分析一致，因此有

从式（2－22）中可见，Aum不受信号频率的影响，对特定电路来说是一个常数。输出电压uo和输入电压ui反相位，相位差为－180°。从图2.65所示中也可看出，电路中频区的频率特性是比较平坦的曲线。

图2.65　单级阻容耦合基本共射放大电路及其频率特性(www.xing528.com)

（2）低频区。若信号的频率f＜fL，称此频率区域为低频区。在低频区，串接在支路中的隔直耦合电容以及旁路电容，如C1、Cb、Ce等，呈现的阻抗增大，信号在这些电容上的压降增大，信号通过时会被明显衰减，增益下降。因此在低频区，不能再视隔直耦合电容以及旁路电容为交流短路；而并接的极间电容和杂散电容，容抗很大，可视为开路。

在低频区，要考虑隔直耦合电容和旁路电容的影响。为使分析简化，这里只考虑耦合电容C1的作用，把耦合电容C2归入后级电路。图2.66所示为单级共射放大电路在低频区的微变等效电路。根据电容C1的阻抗，可计算出在低频区放大电路电压放大倍数的表达式为

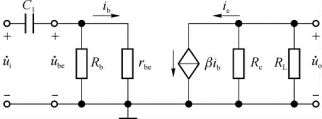
图2.66　单级共射放大电路的低频微变等效电路

定义：

则有：

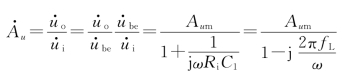
由ω＝2πf，代入并整理得

由式（2－23）可得，电路在低频区的幅频特性和相频特性：

·当f≫fL时，，φ＝－180°。

·当f＝fL时，，φ＝－135°。

·当f≪fL时，，φ＝－90°。

结合图2.65所示可以看出：在低频区，增益随频率的减小而减小；相对于中频区产生超前的附加相位移，相位差φ随着频率的改变而改变。

（3）高频区。若信号的频率f＞fH，则称此频率区域为高频区。在高频区，并接的极间电容和杂散电容容抗减小，对信号产生分流，使增益下降，不可再视为交流开路。串接在支路中的隔直耦合电容和旁路电容呈现的阻抗很小，可视为交流短路。

因此，在高频区主要考虑极间电容的影响。由于极间电容的分流作用，这时三极管的电流放大系数β不再是一个常数，而是信号频率的函数，因此三极管的中频微变等效电路模型在这里不再适用，分析时要用三极管的高频微变模型。有关高频微变模型的内容请参考相关的书籍。

从图2.65所示可见，在高频区，随信号频率的升高，电压增益减小；产生滞后的附加相位移，相位差φ值也随着频率改变。