如图1-4-5(a)所示的电路中:
t<0 时,开关在位置1,电容被电流源充电,电路已处于稳态,电容电压uC(0-)=R0IS;
在t=0 时,开关按箭头方向动作;
在t≥0 时,电容将对R 放电,电路如图1-4-5(b)所示,电路中形成电流i。故t>0 后,电路中无电源作用,电路的响应均是由电容的初始储能而产生,故属于零输入响应。
换路后得图1-4-5(b),根据KVL有uR+uC=0,而![]() 代入上式可得
代入上式可得
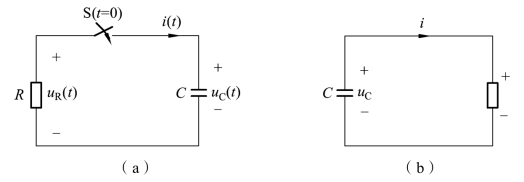
图1-4-5 RC电路的零输入

这是一个一阶齐次方程,根据换路定理,可知初始条件uC(0+)=uC(0-)=u0。方程的通解为
![]()
将初始条件uC(0+)=R0IS代入式(1-4-12),求出积分常数A为
![]()
将uC(0+)代入式(1-4-12),得到满足初始值的微分方程的通解为

放电电流为

令τ=RC,它具有时间的量纲,即

故称τ为时间常数,这样式(1-4-13)、(1-4-15)可分别写为![]() 。
。
由于![]() ,为负,故uC和i均按指数规律衰减,它们的最大值分别为初始值uC(0+)=R0IS,以及
,为负,故uC和i均按指数规律衰减,它们的最大值分别为初始值uC(0+)=R0IS,以及![]() ,当t→∞时,uC和i衰减到零。(https://www.xing528.com)
,当t→∞时,uC和i衰减到零。(https://www.xing528.com)
其变化曲线如图1-4-6所示。
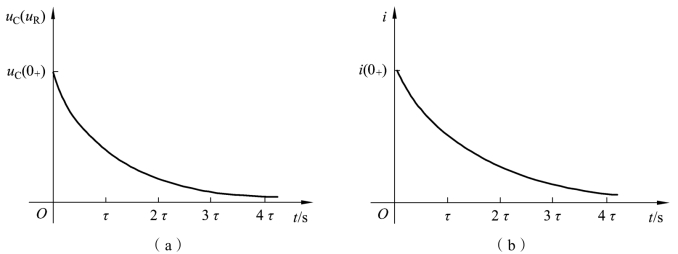
图1-4-6 RC 电路零输入响应电压电流波形图
关于零输入响应曲线的几点说明:
(1)时间常数是体现一阶电路电惯性特性的参数,它只与电路的结构与参数有关,而与激励无关。
(2)对于含电容的一阶电路,τ=RC;对于含电感的一阶电路, 。
。
(3)τ 越大,电惯性越大,相同初始值情况下,放电时间越长。
(4)一阶电路方程的特征根为时间常数的相反数;它具有频率的量纲,称为“固有频率”(natural frequency)。
理论上认为t→∞、uC→0 时,电路达稳态;工程上认为t=(3-5)τ、uC→0,电容放电基本结束。
表1-4-1 列出了电容电压与时间变化之间的数值关系,从中可以看出,理论上需经过无限长时间,电容放电才结束,但工程上认为只要经过4τ~5τ 的时间,电容放电便基本结束。
表1-4-1 电容电压与时间变化的数值关系

【例4.3】如图1-4-7所示,已知t<0 时电路处于稳态,t=0 时开关打开。求t≥0 时的i(t)。

图1-4-7 例4.3 图
解:t<0 时:![]()
t≥0 时,根据换路定律:![]()
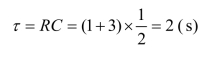
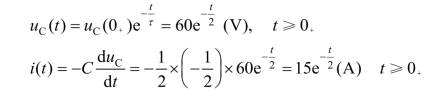
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




