正弦交流电路的计算方法的介绍

一个任意的线性无源单口网络（见图1-2-39），都可以有复阻抗和复导纳两种形式的模型。

（1）复阻抗的定义为

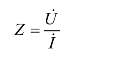
（2）复导纳的定义为

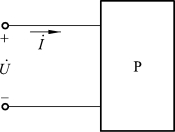
图1-2-39

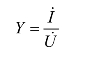
式中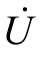，为网络端口的电压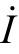；为从端口流入的电流。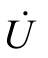和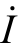的参考方向相关联。

由于同一单口网络的复阻抗和复导纳互为倒数，在计算电阻、电感、电容混联的电路时，可以交替使用复阻抗和复导纳这两种形式进行等效变换或者化简。

【例2.15】计算图1-2-40所示电路ab端口的复阻抗Zab。

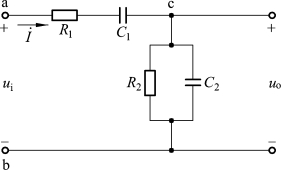
图1-2-40

解：先计算cb端并联部分的复导纳：

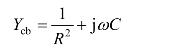
则cb端并联部分的复阻抗为

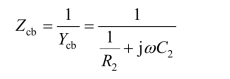
于是ab端的复阻抗为

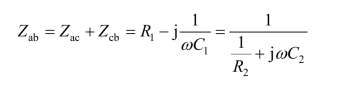
根据上述复阻抗和复导纳的定义，任一线性无源单口网络的电压与电流的关系均可表示为

以上两式即欧姆定律的相量形式。至此，基尔霍夫定律和欧姆定律在正弦交流电路中都有了相应的相量形式。只要把直流电路的电压、电流换成交流电路的电压、电流等相量，把直流电路的电阻、电导换成交流电路的复阻抗、复导纳，那么，在基尔霍夫定律和欧姆定律基础上建立的直流电路的所有公式、定理和分析方法，就全都适用于正弦交流电路的分析计算了。

【例2.16】试分别用节点法、戴维南定理和叠加定理求如图2.41所示电路中的电流。

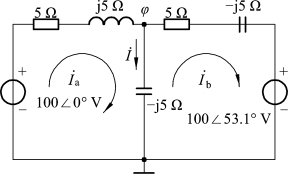
图1-2-41

解：（1）节点法。

设电位参考点为φ，如图所示，列出节点方程为

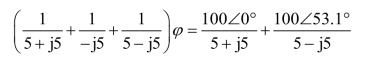(https://www.xing528.com)

解得：

所以，

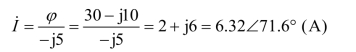
（2）戴维南定理。

去掉电流I˙所在支路，并设开路电压的参考方向如图1-2-42所示。

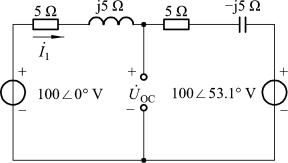
图1-2-42

则：

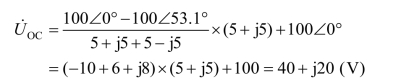
输出阻抗为

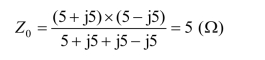
所以，

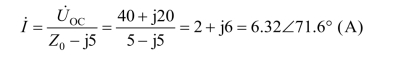
（3）叠加定理。

①100∠0 V电压源单独作用时的电路如图1-2-43所示。

图1-2-43

求得：

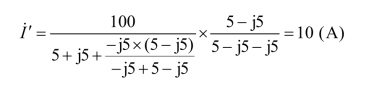
②100∠53.1° V电压源单独作用时的电路如图1-2-44所示。

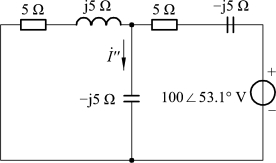
图1-2-44

求得：

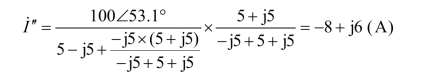
所以，