RLC串联电路原理及应用分析

2.4.1.1　R、L、C串联电路（见图1-2-24）

根据KVL，得：

其中

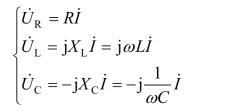
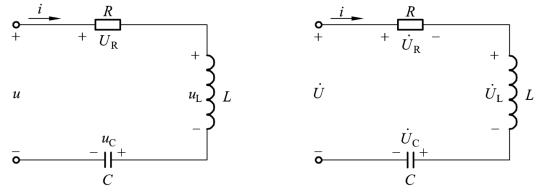
图1-2-24　RLC串联电路

1.电压三角形（见图1-2-25）

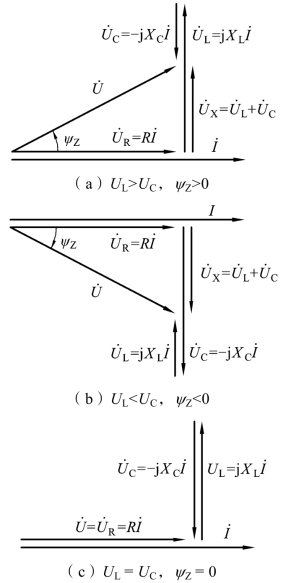
图1-2-25　RLC 串联电路电压三角形

由图1-2-25 分析可知：

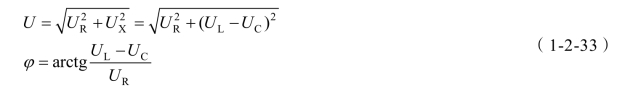
（1）当UL－UC>0，UL>UC，ψZ>0 时，电压超前于电流，电路成电感性，如图1-2-26（a）所示。

（2）当UL－UC<0，UL<UC，ψL>0 时，电压滞后于电流，电路成电容性，如图1-2-26（b）所示。

（3）当UL－UC＝0，UL＝U，ψZ＝0 时，电压与电流同相，电路成电阻性，如图1-2-26（c）所示。

2.　R、L、C 串联电路的VCR相量形式

式中电路的电抗X=XL−XC。

2.4.1.2　复阻抗的定义

在关联参考方向下，正弦交流电路中任意线性无源单口的端口电压相量与电流相量的比称为该单口的复阻抗，用Z表示（见图1-2-26）。即：

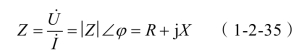
（1）复阻抗的模|Z|即为阻抗，它反映了电路对电流的阻碍作用。

（2）复阻抗的辐角即为阻抗角，反映了电压超前于电流的相位差。

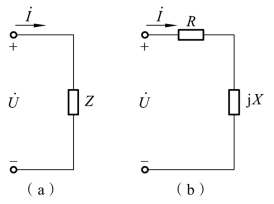
图1-2-26　复阻抗

2.4.1.3　R、L、C串联电路的复阻抗

将电压三角形各边同除电流，就能得到阻抗三角形，其相量图如图1-2-27所示。

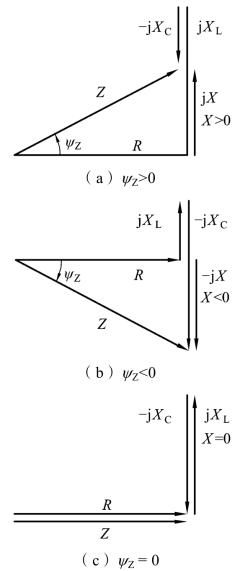
图1-2-27　RLC串联电路的阻抗三角形

阻抗模为(https://www.xing528.com)

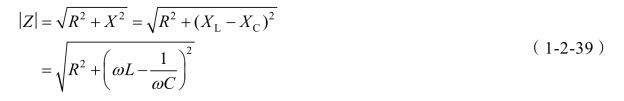
注：任一段电路的电压、电流的相量值，有效值均服从欧姆定律。阻抗角为

表示总电压超前电流的角度。若：

（1）XL>XC，则φ >0，电路呈感性。

（2）XL< XC，则φ<0，电路呈容性。

（3）XL＝XC，则φ＝0，电路呈阻性。

（4）发生谐振，概念另述。

2.4.1.4　任意无源串联单口的复阻抗

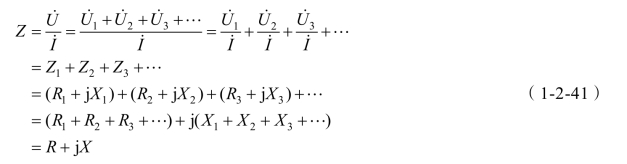
注：

（1）等效复阻抗的计算与电阻的串联类似，但必须用复数计算。

（2）总阻抗的模不等于各分阻抗的模的和。

【例2.12】R、L、C 串联电路如图1-2-28所示。已知：R＝15 Ω、L＝60 mH、C＝25 µF，接正弦电压。

求：电路中的电流i，各元件的电压uR、uL和uC。

解：

各元件的复阻抗分别为

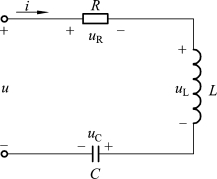
图1-2-28　电路图

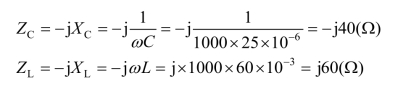
电路的复阻抗：

电路中电流的相量：

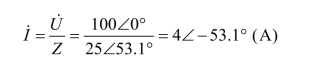
各元件电压的相量：

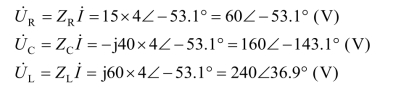
由以上计算结果绘出各电流、电压的相量图（见图1-2-29）及各电流电压的瞬时值表示式分别为

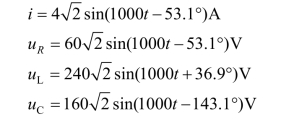
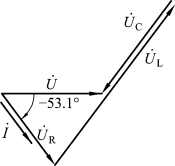
图1-2-29　相量图