复数的概念和运算

1.复数的有关概念和性质

1）虚数单位j

规定 2j1=− ，形如a+bj 的数称为复数，其中a，b∈R。

2）复数的分类（下面的a，b 均为实数）

3）复数的相等

设复数，那么的充要条件是：且 。

4）复数的几何表示

复数z＝a+bj（a，b∈R）可用平面直角坐标系内点Z（a，b）来表示。这时称此平面为复平面，x轴称为实轴，y轴除去原点称为虚轴。这样，全体复数集C与复平面上全体点集是一一对应的。

5）共轭复数

a −bj 称为复数的共轭复数，记为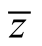，那么z与对应复平面上的点关于实轴对称。且

（1）

（2）

6）复数的模与复数的向量表示

称为复数z=a +bj 的模，记为。复数的模是非负实数。特别。

复数在复平面内还可以用以原点O为起点，以点Z（a ，b）为终点的向量OZ来表示。复数集C和复平面内所有以原点为起点的向量所成的集合也是一一对应的。（例外的是复数0对应点O，看成零向量。）

7）复数与实数的不同

（1）任意两个实数可以比较大小，而任意两个复数中至少有一个不是实数时就不能比较大小。

（2）实数对于四则运算是通行无阻的，但不是任何实数都可以开偶次方.而复数对四则运算和开方均通行无阻。

2.有关计算

（1）怎样计算？（先求n被4除所得的余数，

（2）是1的两个虚立方根，并且：

。

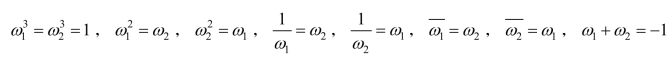（3）复数集内的三角形不等式是：，其中左边在复数对应的向量共线且反向（同向）时取等号，右边在复数z1、z2对应的向量共线且同向（反向）时取等号。

（4）棣莫佛定理是：

（5）若非零复数，则z的n次方根有n个，即：(www.xing528.com)

思考：它们在复平面内对应的点在分布上有什么特殊关系？

答：它们都位于圆心在原点，半径为的圆上，并且把这个圆n等分。

（6）若，复数z1、z2对应的点分别是A、B，则△AOB（O为坐标原点）的面积是。

（7）复平面内复数z 对应的点的几个基本轨迹：

①argz=θ（θ为实常数）↔轨迹为一条射线。

②arg（z −z0）=θ（z0是复常数，θ是实常数）↔ 轨迹为一条射线。

③（r是正的常数）↔ 轨迹是一个圆。

④（z1、z2是复常数）↔轨迹是一条直线。

⑤（z1、z2是复常数，a是 正的常数）↔ 轨迹有三种可能情形：

a）当时，轨迹为椭圆；

b）当时，轨迹为一条线段；

c）当时，轨迹不存在。

⑥（a是 正的常数）↔轨迹有三种可能情形：

a）当时，轨迹为双曲线；

b）当时，轨迹为两条射线；

c）当时，轨迹不存在。

【例2.1】在复平面内，若所对应的点在第二象限，则实数m 的取值范围是（　）

A.(0,3)　B.(−∞, −2)　C.(−2,0)　D.(3,4)

【例2.2】已知z是复数，均为实数（j 为虚数单位），且复数（z+aj）2在复平面上对应的点在第一象限，求实数a 的取值范围。

【例2.3】设a∈R，z∈C，满足（z2－a2）/（z2+a2）是纯虚数，求a，z 应满足的条件。

【例2.4】设复数z＝lg（m2－2m－2）＋（m2＋3m＋2）j，试求实数m 取何值时，①z是纯虚数；②z是实数；③z 对应的点位于复平面的第二象限。

【例2.5】设z∈C，求满足且|z－2|＝2 的复数z。

【例2.6】已知对于任意x∈R 均有|z1|＞|z2|成立，试求实数a 的取值范围。