电压源、电流源及等效变换原理详解

电源可以用两种不同的电路模型来表示：一种是以电压的形式向外供电，称为电压源模型；另一种是以电流的形式向外供电，称为电流源模型。

1.3.2.1　电压源

电压源是一个理想二端元件，其图形符号如图1-1-35（a）所示，uS（t）为电压源电压，“+”“－”为电压的参考极性。电压uS（t）是某种给定的时间函数，与流过电压源的电流无关。因此电压源具有以下两个特点：

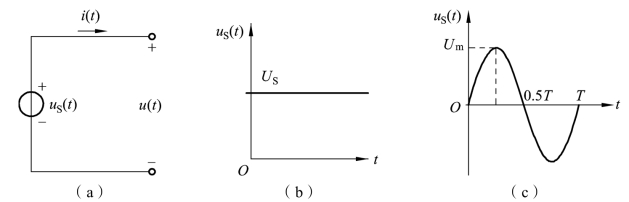
图1-1-35　电压源及其电压波形

（1）电压源对外提供的电压u（t）是某种确定的时间函数，不会因所接的外电路不同而改变，即u（t）＝uS（t）。

（2）通过电压源的电流i（t）随外接电路不同而不同。

图1-1-36是直流电压源的伏安特性，它是一条与电流轴平行且纵坐标为US的直线，表明其端电压恒等于US，与电流大小无关。当电流为零，亦即电压源开路时，其端电压仍为US。

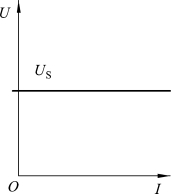
图1-1-36　直流电压源的 伏安特性

如果一个电压源的电压US＝0，则此电压源的伏安特性为与电流轴重合的直线，它相当于短路。即电压为零的电压源相当于短路。由此，我们也可以发现，要使电压源uS（t）对外不输出电压u（t），可将其短路，即起到“置零”的作用。

由图1-1-35（a）可知，电压源的电压uS（t）与流过它的电流i（t）是非关联参考方向，则电压源的功率为

p＝－uS(t)·i(t)

当p<0时，电压源实际上是发出功率，电流的实际方向是从电压源的低电位流向高电位，电压源此时是作为电源存在的；当p>0时，电压源实际上是接收功率，电流的实际方向是从电压源的高电位流向低电位，电压源此时是作为负载存在的。

1.3.2.2　电流源

电流源也是一个理想二端元件，其图形符号如图1-1-37（a）所示，iS（t）为电流源电流，“→”为电流的参考方向。电流iS（t）是某种给定的时间函数，与电流源两端的电压无关。因此电流源具有以下两个特点：

（1）电流源对外提供的电压i（t）是某种确定的时间函数，不会因所接的外电路不同而改变，即i（t）＝iS（t）。

（2）电流源两端的电压u随外接电路不同而不同。

图1-1-38是直流电流源的伏安特性，它是一条与电压轴平行且横坐标为IS的直线，表明其电流恒等于IS，与电压大小无关。当电压为零，亦即电流源短路时，其电流仍为IS。

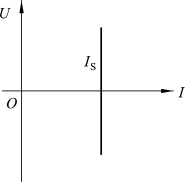
图1-1-38　直流电流源的伏安特性

如果一个电流源的电流IS＝0，则此电流源的伏安特性为与电压轴重合的直线，相当于开路，即电流为零的电流源相当于开路。由此，我们也可以发现，要使电流源iS（t）对外不输出电流i（t），可将其开路，即起到“置零”的作用。

由图1-1-37（a）知，电流源的电流iS（t）与其两端的电压u（t）是非关联参考方向，则电流源的功率为：p＝－u（t）·iS（t）。

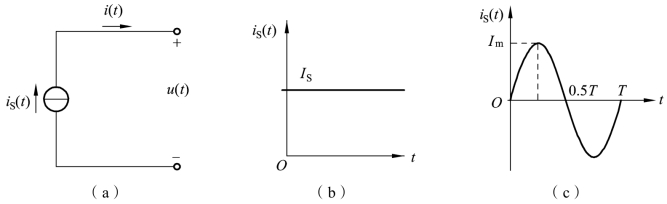
图1-1-37　电流源及其电流波形

当p<0 时，电流源实际上是发出功率，电压的实际方向与其参考方向相同，电流源此时是作为电源存在的；当p>0 时，电流源实际上是接收功率，电压的实际方向与其参考方向相反，电流源此时是作为负载存在的。

上述电压源对外输出的电压为一个独立量，电流源对外输出的电流也为一个独立量，因此二者常被称为独立电源。

1.3.2.3　实际电压源、实际电流源及其等效变换

1.实际电压源、电流源的模型

常见实际电源（如发电机、蓄电池等）的工作原理比较接近电压源，其电路模型是电压源与其内阻的串联组合，如图1-1-39（a）所示。像光电池这类器件，其工作时的特性比较接近电流源，电路模型是电流源与其内阻的并联组合，如图1-1-39（b）所示。

当负载变化时，电路中的电流I 与电源端口电压U 之间的变化关系称为电源的伏安特性。假设一负载RL接于图1-1-39（a）、（b）端口处，构成完整电路，电路中的电流I 与电源端电压U 如该图中所示，则实际电压源和实际电流源模型的伏安特性方程分别为

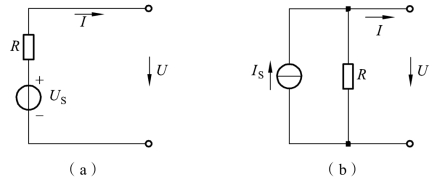
图1-1-39　实际电压源与电流源的模型

和

由式（1-1-24）和式（1-1-25）可分别作出实际电压源和实际电流源模型的伏安特性曲线，如图1-1-40所示。

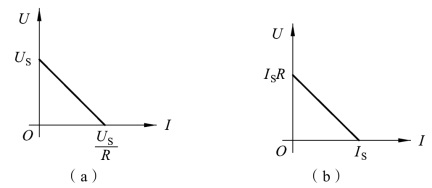
图1-1-40　实际电压源与电流源的伏安特性曲线

2.实际电压源、电流源模型之间的等效变换

在电路分析中，常利用实际电压源与实际电流源模型之间的等效变换，即电压源串联电阻等效变换为电流源并联电阻来化简电路的计算。

根据等效原理，对外电路而言，图1-1-39中的实际电压源与实际电流源模型端口输出的电压U、电流I应大小相等，方向相同，即二者的伏安特性方程一致。比较式（1-1-24）和式（1-1-25）可得二者等效条件为

且二者内阻R相等。(www.xing528.com)

【例1.16】求图1-1-41所示电路的电流I。

解：根据实际电压源与实际电流源等效变换的条件，图1-1-41（a）所示电路可简化为图1-1-41（e）所示单回路电路。简化过程如图1-1-41（b）、（c）、（d）、（e）所示。由化简后的电路可求得电流为

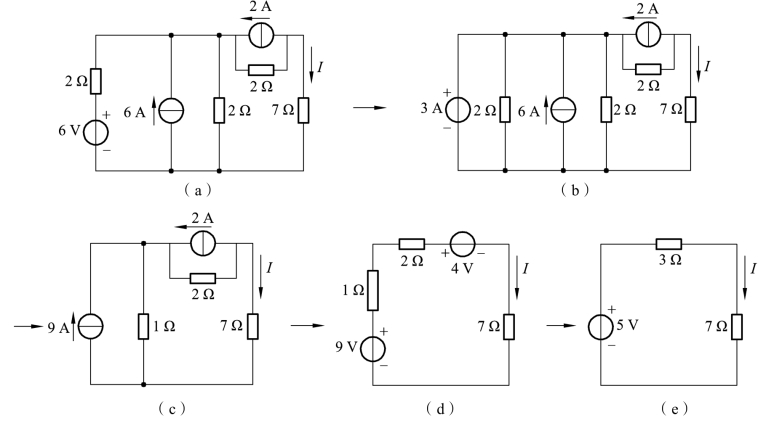
图1-1-41　例1.16图

*1.3.2.4　受控源

1.受控源的概念

电压源和电流源称为独立源。在电子电路的模型中还常常遇到另一种电源，它们的源电压和源电流不是独立的，受电路中另一处的电压或电流控制。

电源的电压或电流受电路中其他部分的电压或电流控制的电源称为受控源，亦称为非独立电源。当控制的电压或电流消失或等于零时，受控源的电压或电流也将为零。受控源由两个支路组成，一个叫控制支路，一个叫受控支路。

如果电路向外连接有两个端子，从一个端子流入的电流恒等于从另一个端子流出的电流，则我们把这两个端子称为一个端口。受控源一般由两个端口构成，一个称为输入端口或控制端，是施加控制量的端口，所施加的控制量可以是电流也可以是电压；另一个称为输出端口或受控端，是对外提供电压或电流的。

输出端是电压的称为受控电压源。受控电压源又按其输入端的控制量是电压还是电流分为电压控制电压源（Voltage Controlled Voltage Source，VCVS）和电流控制电压源（Current Controlled Voltage Source，CCVS）两种。

输出端是电流的称为受控电流源。同样，受控电流源也按其输入端的控制量是电压还是电流分为电压控制电流源（Voltage C ontrolled C urrent S ource，VCCS）和电流控制电流源（Current Controlled Current Source，CCCS）两种。

受控源就是从实际电路中抽象出来的四端理想电路模型。例如：晶体三极管工作在放大状态时，其集电极电流受到基极电流的控制；运算放大器的输出电压受到输入电压的控制。这些都可以看成是受控源，器件的某些端口电压或电流受到另外一些端口电压或电流的控制，并不是独立的，因此，又把受控源称为非独立电源。

按受控源的端口电压和电流关系可作以下分类。

（1）电压控制电压源（VCVS）：

（2）电流控制电压源（CCVS）：

（3）电压控制电流源（VCCS）：

（4）电流控制电流源（CCCS）：

式中，µ、r、g、α是控制系数。其中，µ 和α 无量纲，r 和g 分别具有电阻和电导的量纲。当这些系数为常数时，被控电源数值与控制量成正比。这种受控源称为线性受控源。本书只涉及这类受控源。图1-1-42 分别给出了这四种受控源的电路符号。

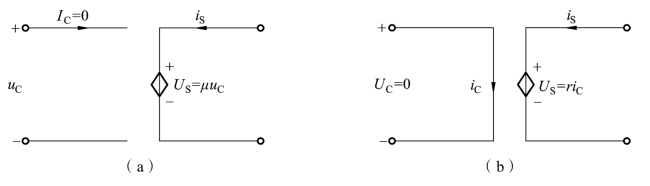
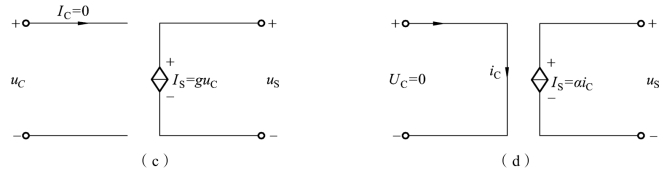
图1-1-42　受控源的四种形式

受控源有两个端口，但由于控制口功率为零，端口不是开路就是短路。因此，在电路图中，不一定要专门画出控制口，只要在控制支路中标明该控制量即可。如图1-1-43所示，两种画法本质上是相同的，但图（a）更简单明了。

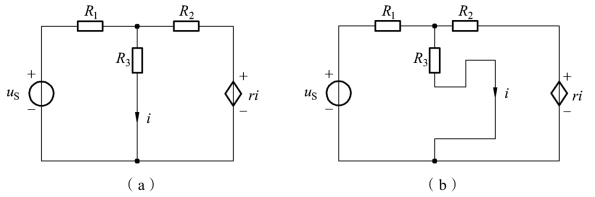
图1-1-43　含受控源的电路

2.含受控源电路的分析

互连约束和元件的电压电流关系是分析计算电路的基本依据。以上介绍的各种方法和定理都可用来计算有受控源的电路，即把受控源先按独立源对待，但又必须掌握受控源是非独立源这一特点。下面简要介绍含受控源电路的特点。

（1）受控电压源和电阻串联组合与受控电流源和电阻并联组合之间，像独立源一样可以进行等效变换。但在变换过程中，必须保留控制变量的所在的支路。

（2）应用网络方程法分析计算含受控源的电路时，将受控源按独立源一样对待和处理，但在网络方程中，要将受控源的控制量用电路变量来表示。

（3）用叠加定理求每个独立源单独作用下的响应时，受控源要像电阻那样全部保留。同样，用戴维南定理求网络去除源后的等效电阻时，受控源也要全部保留。

（4）含受控源的二端电阻网络的等效电阻可能为负值，这表明该网络向外部电路发送能量。

【例1.17】如图1-1-44所示，iS＝2 A，VCCS的控制系数g＝2 S，求u。

解：由图1-1-44左部先求控制电压u1。

图1-1-44　例1.17图

u1＝5iS＝5×2＝10（V）

故

i＝gu1＝2×10＝20（A）

则求得u为

u＝2i＝2×20＝40（V）