电阻的串并联及混联处理方法

1.3.1.1　电阻的串联

在电路中，把几个电阻元件依次首尾相连接，中间没有分支，在电源的作用下流过各电阻的是同一电流。这种连接方式叫作电阻的串联，如图1-1-24所示。

图1-1-24　电阻的串联

1.电阻串联电路的特点

设总电压为U、电流为I、总功率为P。

（1）等效电阻： R＝R1+R2+… +Rn

（2）分压关系：

（3）功率分配：

特例：两只电阻R1、R2串联时，等效电阻R＝R1+R2，则有分压公式

2.应用举例

【例1.9】有一盏额定电压U1＝40 V、额定电流I＝5 A 的电灯，如何把它接入电压U＝220 V 照明电路中？

解：将电灯（设电阻为R1）与一只分压电阻R2串联后，接入U＝220 V 电源上，如图1-1-25所示。

解法一：分压电阻R2上的电压为

U2＝U－U1＝220－40＝180 V，且U2＝R2I，则

解法二：利用两只电阻串联的分压公式，且，可得

即将电灯与一只36 Ω 分压电阻串联后，接入U＝220 V 的电源上即可。

【例1.10】有一只电流表，内阻Rg＝1 kΩ，满偏电流为Ig＝100 µA，要把它改成量程为Un＝3 V 的电压表，应该串联一只多大的分压电阻R？

解：如图1-1-26所示。

该电流表的电压量程为Ug＝RgIg＝0.1 V，与分压电阻R 串联后的总电压Un＝3 V，即将电压量程扩大到n＝Un/Ug＝30 倍。

利用两只电阻串联的分压公式，可得，则

上例表明，将一只量程为Ug、内阻为Rg的表头扩大到量程为Un，所需要的分压电阻为R＝（n－1）Rg，其中n＝（Un/Ug）称为电压扩大倍数。

1.3.1.2　电阻的并联

在电路中，把几个电阻元件的首尾两端分别连接在两个节点上，在电源的作用下，它们两端的电压都相同，这种连接方式叫作电阻的并联。如图1-1-27所示。

图1-1-25　例1.9 图

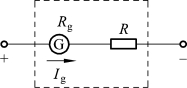
图1-1-26　例1.10 图

1.电阻并联电路的特点

设总电流为I、电压为U、总功率为P。

（1）等效电阻：

（2）分流关系：R1I1＝R2I2＝…＝RnIn＝RI＝U

（3）功率分配：R1P1＝R2P2＝…＝RnPn＝RP＝U2

特例：两只电阻R1、R2并联时，等效电阻，则有分流公式：

图1-1-27　电阻的并联

2.应用举例

【例1.11】如图1-1-28所示，电源供电电压U＝220 V，每根输电导线的电阻均为R1＝1 Ω，电路中一共并联100盏额定电压为220 V、功率为40 W的电灯。假设电灯在工作（发光）时电阻值为常数。试求：（1）当只有10盏电灯工作时，每盏电灯的电压UL和功率PL；（2）当100盏电灯全部工作时，每盏电灯的电压UL和功率PL。

图1-1-28　例1.11图

解：每盏电灯的电阻为R＝U2/P＝1210 Ω，n盏电灯并联后的等效电阻为Rn＝R/n。

根据分压公式，可得每盏电灯的电压

功率

（1）当只有10盏电灯工作时，即n＝10，则Rn＝R/n＝121 Ω，因此

（2）当100盏电灯全部工作时，即n＝100，则Rn＝R/n＝12.1 Ω，

【例1.12】有一只微安表，满偏电流为Ig＝100 µA、内阻Rg＝1 kΩ，要改装成量程为In＝100 mA的电流表，试求所需分流电阻R。

解：如图1-1-29所示，设n＝In/Ig（称为电流量程扩大倍数），

图1-1-29　例1.12图

根据分流公式可得则

本题中n＝In/Ig＝1 000，

上例表明，将一只量程为Ig、内阻为Rg的表头扩大到量程为In，所需要的分流电阻为R＝Rg/（n－1），其中n＝（In/Ig）称为电流扩大倍数。

1.3.1.3　电阻的混联

在电阻电路中，既有电阻的串联关系又有电阻的并联关系，称为电阻混联。

1.分析步骤

对混联电路的分析和计算大体上可分为以下几个步骤：

（1）首先整理清楚电路中电阻串、并联关系，必要时重新画出串、并联关系明确的电路图。

（2）利用串、并联等效电阻公式计算出电路中总的等效电阻。(www.xing528.com)

（3）利用已知条件进行计算，确定电路的总电压与总电流。

（4）根据电阻分压关系和分流关系，逐步推算出各支路的电流或电压。

2.解题举例

【例1.13】如图1-1-30所示，已知R1＝R2＝8 Ω，R3＝R4＝6 Ω，R5＝R6＝4 Ω，R7＝R8＝24 Ω，R9＝16 Ω；电压U＝224 V。试求：

图1-1-30　例1.13 图

（1）电路总的等效电阻RAB与总电流IΣ；

（2）电阻R9两端的电压U9与通过它的电流I9。

解：（1）R5、R6、R9三者串联后，再与R8并联，E、F两端等效电阻为

REF＝(R5+R6+R9)∥R8＝24 Ω∥24 Ω＝12 Ω

REF、R3、R4三者电阻串联后，再与R7并联，C、D两端等效电阻为

RCD＝(R3+REF+R4)∥R7＝24 Ω∥24 Ω＝12 Ω

总的等效电阻 RAB＝R1+RCD+R2＝28 Ω

总电流　IΣ＝U/RAB＝224/28＝8（A）

（2）利用分压关系求各部分电压：

【例1.14】如图1-1-31所示，已知R＝10 Ω，电源电动势E＝6 V，内阻r＝0.5 Ω，试求电路中的总电流I。

解：首先整理清楚电路中电阻串、并联关系，并画出等效电路，如图1-1-32所示。四只电阻并联的等效电阻为

Re＝R/4＝2.5 Ω

根据全电路欧姆定律，电路中的总电流为

图1-1-31　例1.14图

图1-1-32　例1.14的等效电路

1.3.1.4　电阻的星形连接、三角形连接及其等效变换

1.电阻的星形（Y形）连接和三角形（△形）连接

3个电阻元件首尾相连，连成一个三角形，就叫作三角形连接，简称△形连接，如图1-1-33（a）所示。3个电阻元件的一端连接在一起，另一端分别连接到电路的3个节点，这种连接方式叫作星形连接，简称Y形连接，如图1-1-33（b）所示。

图1-1-33　电阻的三角形和星形连接

2.电阻的星形连接和三角形连接的等效变换（Y-△等效变换）

在电路分析中，常利用Y 形网络与△形网络的等效变换来简化电路的计算。根据等效网络的定义，在图1-1-32所示的Y 形网络与△形网络中，若电压U12、U23、U31和电流I1、I2、I3都分别相等，则两个网络对外是等效的。据此，可导出Y 形连接电阻R1、R2、R3与△形连接电阻R12、R23、R31之间的等效关系。

将KVL 应用于图1-1-33（a）中的回路1231，得

R12I12+R23I23+R31I31＝0

由KCL 得 I23＝I2+I12

I31＝I12－I1

代入上式，得 R12I12+R23（I2+I12）+R31（I12－I1）＝0

经过整理后，得

同理可求得

对于图1-1-33（b）有

比较式（1-1-17）和式（1-1-18）可得：若满足等效条件，两组方程式I1、I2、I3前面的系数必须相等，即

式（1-1-20）就是从已知的△形连接电阻变换为等效Y 形连接电阻的计算公式。解方程组式（1-1-20），可得

式（1-1-21）就是从已知的Y形连接电阻变换为等效△形连接电阻的计算公式。

若△形（或Y形）连接的3个电阻相等，则变换后的Y形（或△形）连接的3个电阻也相等。设△形3个电阻R12＝R23＝R31＝R△，则等效Y形的3个电阻为

反之

【例1.15】在图1-1-34（a）所示电路中，已知US＝225 V，R0＝1 Ω，R1＝40 Ω，R2＝36 Ω，R3＝50 Ω，R4＝55 Ω，R5＝10 Ω，试求各电阻的电流。

图1-1-34　例1.15图

解：将△形连接的R1、R3、R5等效变换为Y形连接的RA、RC、RD，如图1-1-33（b）所示，代入式（1-1-20）求得

图1-1-34（b）是电阻混联网络，串联的RC、R2的等效电阻RC2＝40 Ω，串联的RD、R4的等效电阻RD4＝60 Ω，二者并联的等效电阻

RA与ROB串联，A、B 间桥式电阻的等效电阻 Ri＝20+24＝44（Ω）

桥式电阻的端口电流

R2、R4的电流各为

从图1-1-34（b）求得

UAC＝RAI+RCI2＝20×5+4×3＝112(V)

回到图1-1-34（a）电路，利用KCL 可求得流过R1、R3和R5的电流