指标符号运算约定及张量阶数的计算方法

1.求和约定

如有方程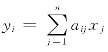，引入求和约定后，写成

其中i为自由指标，j为哑元，表示哑元的指标可任意改变，式（1）也可写成yi＝aimxm，但同一项中不允许同一指标出现三次或三次以上。

按照该求和约定，矢量的点乘a·b＝aibi（i＝1，2，3）。

散度，即

这里下角标中的“，”表示微分号“∂”。

Laplace方程可写为

高斯（gauss）积分定理

其中，ni为曲面S上某点的外法线余弦分量。

分部积分公式

2.δij函数

δij函数即克罗内克（Kronecker delta）函数，其定义为

按照求和约定，显然有δimδmj＝δmiδjm＝δij；δijδij＝δii＝3（i＝1，2，3）。

3.排列符号

排列符号与δij函数的关系式为

在笛卡尔坐标中的矢量a的分量为ai，单位基矢量为ei。

矢量的叉乘a×b＝cijkajbkei；旋度为

斯托克斯（Stoke's）定理可写为

其中，称为矢量a的环量。

定义矢量算子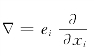：，有下列表达式(www.xing528.com)

并有如下关系式

4.张量的定义

当一个变量在坐标系变换时，在坐标系内的分量之间的变换服从统一的规律，即满足

关系的集合为张量。这种规律称为张量不变规律。式中i，j为自由指标，m，n为哑元指标，转换系数βmi，βnj，βim和βjn为新坐标轴与原坐标轴间的方向余弦，其中第一个右下标代表新坐标轴轴号，第二个右下标代表原坐标轴轴号。

张量tij变换到新坐标中时，需要乘二次转换系数，坐标转换时需乘转换系数的个数，称为张量的阶数，也是分量指标的个数。比如tijk是三阶张量，tij是二阶张量，矢量为一阶张量，标量为零阶张量。

直角坐标变换

式（14）和式（15）的系数βij为正交矩阵，满足关系式βikβjk＝δij；βkiβkj＝δij。

可用类似矢量的形式直接表示张量，如用T表示张量，Tij表示张量T的分量，写成如下并矢的形式

其中，ek⊗el为基矢量的并矢，称为基张量。定义基张量为I＝δklek⊗el。式（16a）的定义可推广的任意阶张量。设T为m阶张量，S为n阶张量，则有

5.张量的代数运算

两张量相等：A＝B，则，即张量的每个分量相等。

两张量相加：S＝A+B，则，即张量的对应分量相加。

标量a与张量A相乘：S＝aA，有

对称张量：Tij＝Tji；反对称张量：Tij＝－Tji；球张量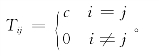

矢量u与张量T的点积为

张量T与张量S的点积为

张量T与张量S的双点积为

如果T＝I，则有I∶S＝δklSkl＝Skk。