程序代码优化后的数值模拟实验

为测试算法改进与程序优化的效果，本节针对三级配混凝土标准试件进行静载弯拉数值模拟试验，试件尺寸为300mm×300mm×1100mm，采用三分点加载法（DL/T 5150—2001，2002）。

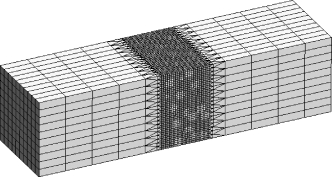
图13.1　三级配混凝土试件有限元网格

采用与图12.2类似的网格剖分方法对整个试件进行有限元离散。整体上采用八结点六面体等参元，在网格点较密区域与较稀区域的交界区域，采用常应变四面体单元过渡。对整个试件的离散，共有53200个单元、44117个结点，如图13.1所示。对线性方程组的求解实际上是求每一加载步上各个网格点上位移的变化量，而每个结点的位移可分解为三个方向的分位移，所求解的每个稀疏线性方程组大约在13万阶左右。下面针对这个问题，介绍在一台主频为2.6GHz、内存为1G的微机上进行数值试验的结果。

当采用前述的对角优势强化技术与预条件迭代相结合来求解稀疏线性方程组，线性迭代终止条件取为残向量的2范数下降10个数量级，初始解向量利用预条件来计算，同时对程序采用优化技术，但整体刚度矩阵仍然采用原来程序中的分块技术来进行装配时，进行一次加载计算的时间从11442s减少到180s。在这180s内，预条件构造时间为20s，线性方程组求解时间为38s，整体刚度矩阵的装配时间占总时间中的大部分。当对整体刚度矩阵的装配采用文中所提出的算法时，一次加载的计算时间可以再降为90s左右，相对原程序而言，加速了127倍。由此可见，不只是稀疏线性方程组的求解十分重要，刚度矩阵的装配也是很重要的，特别是在设计并行算法时，如果不采用高效的并行算法，由于在对稀疏线性方程组的求解算法进行改进后，刚度矩阵的装配所需时间所占的比重已经相当大，所以必将严重影响并行计算的效果。(www.xing528.com)

在求解线性方程组时，预条件的选取对计算时间的影响也是十分明显的，在表13.1中列出了进行一次加载计算时，不采用预条件和采用SSOR预条件（Saad，1996）、ILU（0）预条件（Saad，1996）与ICT预条件（吴建平，2004、2005）时的预条件构造时间、预条件迭代次数、预条件迭代时间的比较。从表13.1中可以看出，在没有采用预条件时，采用CG法需要迭代2083次，所以计算时间也比较长。在采用预条件技术后，迭代次数可以大幅度缩减，从而求解时间也得以有效减少。ILU（0）预条件优于SSOR预条件，同时，单纯从一次加载来看，ICT预条件构造时间与迭代时间之和比ILU（0）预条件小不了多少，这似乎说明ICT预条件与ILU（0）预条件相当，但可以发现，虽然ICT预条件的构造时间较长，但ICT预条件的迭代时间比ILU（0）时短得多，而在具体进行数值模拟时，如果尚没有单元损伤，则整体刚度矩阵在第一次装配完毕之后一直不变，所以在单元发生损伤之前，实际上只需要在第一次加载时构造预条件，后续多次加载都只需要重用该预条件即可。如果单元发生损伤，则在每次加载计算时，虽然加载时需要重新装配刚度矩阵，但对同一次加载需要反复求解系数矩阵等于该刚度矩阵的稀疏线性方程组，所以也只要在形成刚度矩阵时构造一次预条件。这就说明，从实际计算的角度来说，采用ICT预条件的效果将会大大优于ILU（0）预条件。

表13.1　多种预条件的效果比较

需要说明的是，由于对程序中刚度矩阵装配与稀疏线性方程组算法的改造并没有影响到整个数值模型中其他算法，而这些改进后的算法的计算结果与改进前的算法几乎可以一致，所以实际上整体计算结果也几乎与原算法一致。此外，在这里的试验中，线性方程组迭代求解的终止条件取为残向量2范数下降10个数量级，这对精度的要求已经很高，实际上采用下降4个数量级时，得到的应力—应变曲线已经与原算法的计算结果完全一致。从这个意义上说，采用的技术改进效果明显。同时，值得注意的是，变带宽算法是不便于并行处理的，而采用迭代法在并行计算时将更具优势。