基于双尺度方法的优化多尺度算法

前面提到的具有多种尺度颗粒随机分布的复合材料，它的期望均匀化参数（等效力学性能参数）可以用经典的有限元方法进行计算，但用此方法进行计算时有如下的困难：颗粒太多，因而用数值方法进行模拟时很难生成颗粒和网格。为了减少计算机模拟和计算期望均匀化参数的复杂性，按照具有多种尺度颗粒的周期性，把颗粒的尺寸分成m尺度，然后确定每个颗粒在当前尺度下的分布，逐级生成整个材料，用双尺度方法去递归地计算最终的期望均匀化性能参数。

下面将给出利用双尺度算法计算多种尺度颗粒的复合材料的等效力学性能参数的求解步骤（崔俊芝，2004）：在这里以只有一种骨料的复合材料为例，首先假设基体材料的力学参数为{aijhk}，颗粒增强材料的力学参数为{a′ijhk}。

（1）计算第m尺度下的期望均匀参数

1）基于m尺度颗粒的统计规律，∀ωs，具有颗粒的样本被生成，它的力学性能参数在εmQs（εm）可以被定义为

式中：是基体材料；是颗粒增强材料。

2）从材料系数}并通过用有限元解方程式（12.15）得到），然 后 通 过 式（12.24）可 以 得 到 此 样 本 的 均 匀 化 系数}。

3）对ωs∈P， s＝1，2，…，Mm，1）和2）重复Mm次，可得到Mm个均匀化系数（s＝1，2，…，Mm）。这样就可以预测具有颗粒尺度小于εm的期望均匀化系数。(www.xing528.com)

（2）如果r＝m－1，m－2，…，1，可以按递归的方法求出每个尺度的均匀化系数

1）基于第r尺度的颗粒分布特性的统计规律得到颗粒各种参数的分布形式，然后用计算机模拟得到它的样本ωs，从而可以得到材料力学性能参数，且是随机变量的一个样本，即

式中：是基体材料；是颗粒增强材料。

2）从材料系数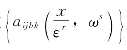，并通过用有限元解方程式（12.15）的变分形式可以得到，然后通过式（12.24）可以得到此样本的均匀化系数

3）对ωs∈P， s＝1，2，…，Mr，1）和2）重复Mr次，可得到Mr个均匀化系数（s＝1，2，…，Mr）。这样就可以计算具有颗粒尺度小于εr的期望均匀化系数。

（3）最后，均匀化系数是在Ω上的期望均匀化系数（等效力学性能参数）。