多尺度算法基本理论简介

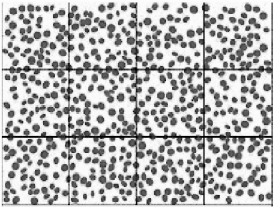
图12.5　具有同一尺度颗粒分布的统计区域Ω

预测复合材料力学性能参数的多尺度算法是基于双尺度的循环递推。双尺度复合材料是由基体和具有同一尺度范围的颗粒组成，整个区域的结构Ω可以逻辑地分解成一系列其尺寸ε远大于所含颗粒的最大尺寸的、作为统计窗的单胞体εQs的集合。每个单胞体中颗粒概率分布相同，因而也就等于整个结构的颗粒概率分布。设ωs为统计窗内颗粒随机参数分布的一个样本，ωs∈P（样本空间），如图12.5所示，则样本集ω＝{ωs/x∈εQs⊂Ω}。

两相材料的双尺度分析方法中的力学参数，可通过周期性随机分布，并将其一个样本的力学参数表示为

式中：εQs是统计窗区域；ei1表示在εQs中的i1个椭球颗粒；N表示在统计窗中的最大颗粒数；和是给定范围内的正常数，并且正定、对称，并在统计区域Ω内的期望均化值有界。

显然，是一个可测的随机变量集。同时假定Ω区域是具有同尺度颗粒小周期性随机分布的复合材料区域，即，（Z为整数向量空间），如图12.5所示。为了获取具有小周期性颗粒随机分布复合材料的等效力学参数，可以考虑如下弹性问题

式中：uε（x，ω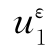）＝[（x，ω），（x，ω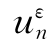），…，（x，ω）]；x＝[x1，x2，…，xn]；∂Ω表示区域Ω的边界；i，j，h，k＝1，2，…，n。

用构造的方法在每一个单胞εQs上建立双尺度公式去计算等效力学参数（期望均匀化系数）。先假设此处存在一组力学参数在整个区域Ω中满足椭圆性条件，而且向量值函数u0（x）是如下问题的解

此处u0（x）被称为在Ω上的期望均匀化解，在Ω内的期望均匀化系数，可以证明其满足对称性和正定性。

对每一个ωs样 本，式（12.2）有唯一解uε（x，ω），从 弹 性 方 程式（12.2）可知位移uε（x，ω）和应力依赖于整体结构Ω和在每一个单胞体εQs的微观分布，所以位移可以表示为uε（x，ω）＝uε（x，ξ，ω），x表示整体结构的性能和行为，，ξ＝[ξ1，ξ2，…，ξn]，表示Qs中的局部坐标以及随机结构的影响。

为了获取随机颗粒分布的复合材料力学性能参数的双尺度格式，可假定uε（x，ω）有如下展开式

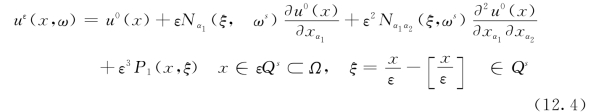
此处是函数矩阵，分别表示为

从式（12.5）和式（12.6）可得

式中：h，α1，α2，m＝1，2，…，n。

由于，考虑到

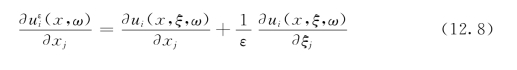
将式（12.7）和式（12.8）代入式（12.2）就可得出ε从－1阶到2阶按升幂排列的表达式为

既然对于任意的ε＞0，式（12.9）都成立，比较方程两边εl（l＝－1，0，1，…）的系数，可以得到如下方程

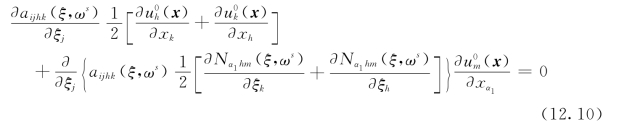
充分利用}的对称性，由式（12.10）可得到

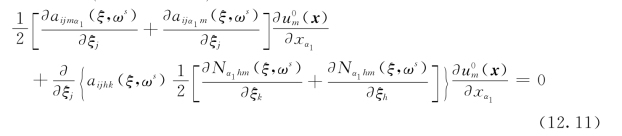
注意到在Ω上不恒等于0，并且材料参数在每一个单胞上相互独立，则有如下方程成立(www.xing528.com)

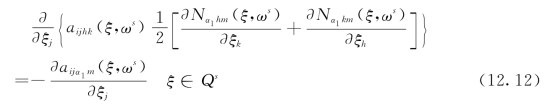
式中：m，α1＝1，2，…，n。令

为了在Qs唯一地定义出Nα1m（ξ，ωs），因此有必要指定边界条件。在这里由于为了满足uε（x，ω）在式（12.2）中的边界条件，非常有必要选择如下边界条件

这样，对任意ωs，在每一个Qs上，得到如下边值方程

上述方程的解存在唯一。既然ε从－1阶到2阶按升幂排列，方程右边独立于ε，则设方程左边ε0的系数等于fi（x）有

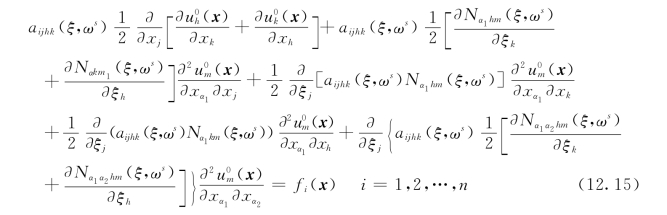
由于{aijhk（x，ω）}对称和正定，即满足aijhk（x，ω）＝ajihk（x，ω）＝aijkh（x，ω），并考虑到均匀化式（12.3），则式（12.15）可以重写为

在式（12.16）中，由于的对称性，可以获得如下方程

考虑到式（12.3），可以获得

既然（α1，α2，m＝1，2，…，n）不总是等于零，且在每个单胞上的材料参数彼此独立，则下式成立

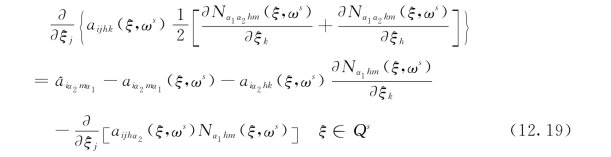
为了独立地定义在Qs中的，同前，指定

对于任意的ωs，在单胞Qs中可以获得如下问题

当s≠t时，虽然Qs和Q t属于同一概率分布，但是彼此独立，对于一个确定的 样 本ωs，则aijhk（ξ，ωs），和不 同 于aijhk（ξ，ωt），和。同时也容易看出aijhk（ξ，ωs），和是可测的随机变量。

式（12.21）描述的是每一个单胞体中的材料特性，由于εQs单胞中随机参数服从平稳随机分布，因此从统计的意义上，上述方程在εQs上的两边积分的期望等于零，从而在此假设上述方程右边在εQs上的积分期望值等于零，则可以得到如下方程

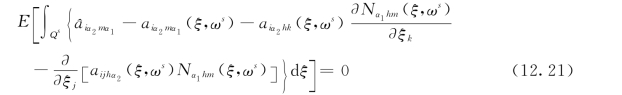
考虑式（12.14）固定边界条件，很显然有

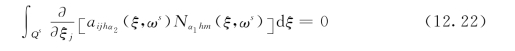
令

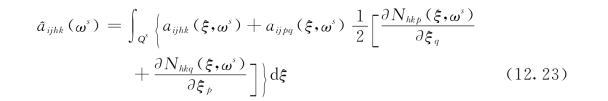
如果的期望值存在，可以得到M个样本期望均匀化参数