混凝土应变率敏感性对动弯拉强度的影响

为了进一步弄清应变率对试件弯拉破坏过程及其动弯拉强度的影响，下面将对混凝土的动弯拉强度及静动综合弯拉强度的应变率强化规律进行应变率敏感性分析，即按一定规律取不同弹性模量强化参数和不同抗拉强度强化参数计算混凝土的动弯拉强度及静动综合弯拉强度，并探寻它们的变化规律。

10.3.3.1　Ht和HE对动弯拉强度的影响

在求强度强化系数Ht及弹性模量强化系数HE的式（8.2）中，当（AE，At）分别取（0.12，0.16）、（0.14，0.18）和（0.16，0.20）时，计算出相应的动强度，以及在预静载分别为静极限荷载20%、40%、60%和80%时系列混凝土的静动综合弯拉强度，其系列相对值如图10.6所示。从图10.6可看出，随着强化参数AE、At的增加，即随着动强度、动弹性模量对应变率敏感性的增加，混凝土的动弯拉强度也在增加，从114.1%、116.9%增加到122.5%；另外，随着该参数值的增加，不同初始静载的动强度也在增加，如对应80%初始静载的动强度从117.3%、122.9%增加到125.7%。总体看，随着动强度、动弹性模量对应变率敏感性的增加，动强度升高，静动综合弯拉强度受预静载水平的影响增强。另外，随着强化参数At、AE的增加，静动综合弯拉强度的峰值所对应的预静载水平有所不同，这也说明，静动综合弯拉强度是率敏感性强化与损伤劣化共同作用的结果。

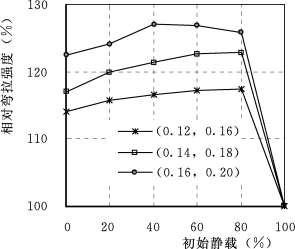
图10.6　率敏感性对静动综合弯拉强度的影响

10.3.3.2　HE取固定值时Ht对动弯拉强度的影响

弹性模量强化参数AE取0.12不变，强度强化参数At分别取0.16、0.18和0.20，计算动强度以及预静载为静极限荷载的20%、40%、60%和80%时的静动综合弯拉强度，如图10.7所示。动强度随着At增加而增大，静动综合弯拉强度对初始预静载的敏感性提高。在At＝0.16时动强度相对值为114.1%；At＝0.18时动强度相对值为118.3%；At＝0.20时动强度相对值为122.5%。显然，动强度和对应于相同预静载下的静动综合弯拉强度随着强度强化参数At的增大而提高，即混凝土试件的弯拉强度随着混凝土材料本身强度的率敏感性增强而提高。图10.8给出了在几种强度强化参数下的应力—位移曲线。从图10.8中看出，在弹性模量强化参数不变的情况下，这些曲线的斜率基本不变，即试件的抗弯刚度基本不变，仅动强度随着强度强化参数增大而提高。

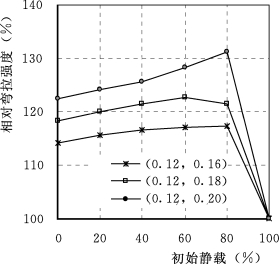
图10.7　强度率敏感性对静动综合弯拉强度的影响(www.xing528.com)

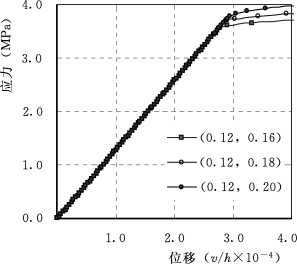
图10.8　强度率敏感性对动弯拉强度的影响

10.3.3.3　Ht取固定值时HE对动弯拉强度的影响

强度强化参数At取0.20保持不变，弹性模量强化参数AE分别取0.12、0.14和0.16，计算动强度以及预静载分别为静极限荷载的20%、40%、60%和80%的静动综合弯拉强度，如图10.9所示。图10.9显示，在强度强化参数不变的情况下，随着弹性模量的率敏感性增强，预静载水平对静动综合弯拉强度的影响降低；而图10.10所示的应力—位移曲线随着AE增大变陡，即弯曲刚度增大。可从混凝土材料的物理性质解释为，强度不变，在同样的荷载（静载+动载）作用下刚度较小的试件变形较大，应变较大，率效应较明显。静动综合弯拉强度因率效应增强而提高，由此可推知，刚度较小而强度较大材料的静动综合弯拉强度对预静载水平敏感性较强。

通过图10.9和图10.10的应力—位移曲线可看出，动载强度主要由混凝土材料的强度率敏感性决定，而动弹性模量主要受混凝土材料的弹性模量率敏感性影响。

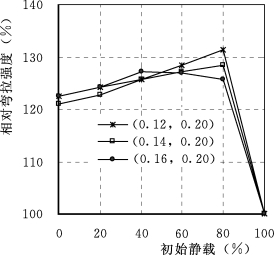
图10.9　弹性模量敏感性对静动综合弯拉强度的影响

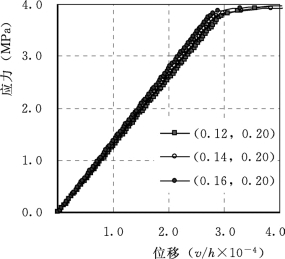
图10.10　弹性模量率敏感性对动弯拉强度的影响